Big O termini haqida

Oldingi maqolada biz Θ (theta) qiymatlarini ya’ni best case va worst caseni topishni ko’rib chiqdik. Best case yana lower bound ham deyiladi, Worst case – upper bound.

Algoritm complexity’ni aniqlashda ko’pincha upper bound’ni topishga e’tibor beriladi. Ana shu upper bound – Big O, uni topish – Big O ni topish deyiladi. Linear search’da ko’rib chiqqanimiz lower bound – 1, upper bound N bo’lsa, Big O = N bo’ladi. Yozilishi – O(n).

Nima uchun upper bound’ga e’tibor beriladi? Sababi lower bound qiymati upper bound ichida bo’ladi baribir. Masalan, Insertion sort uchun lower bound O(n), upper bound O(n²), bunda O(n²) o’z ichiga O(n) ni ham olgan bo’ladi.

Savol, ba’zi algoritmlarda bir necha sikllar, amallar ishlatilgan bo’ladi, u holda time complexity qanday qilib topiladi?

Misol:

function test(arr) {
  const a = b + c
  const N = arr.length
  const K = 123 // Some value

  for (let i = 0; i < N; i++) {
    ...
  }
  ...
  for (let i = 0; i < K; i++) {
    for (let j = 0; j < K; i++) {
      ...
    }
  }
}

Oddiy amallar, matematik amallar, agar ular rekursiya, sikl, yoki boshqa funksiyaga bog’lanmagan bo’lsa, «constant» bo’lib O(1) ga teng bo’ladi.

Sikllarda qadamga qaraladi. Birinchi sikl 0 dan N gacha, demak linear, ya’ni O(n). Ikkinchi, ikkitalik siklda qadamlar soni O(n²) teng, ya’ni quadratic.

Ketma-ket amallar qo’shib yoziladi: f(1 + n + k²)

Bundan time complexity ni topish uchun constant’lar tushirib qoldiriladi. Demak yuqoridagi funksiya uchun time complexity O(n + k²).

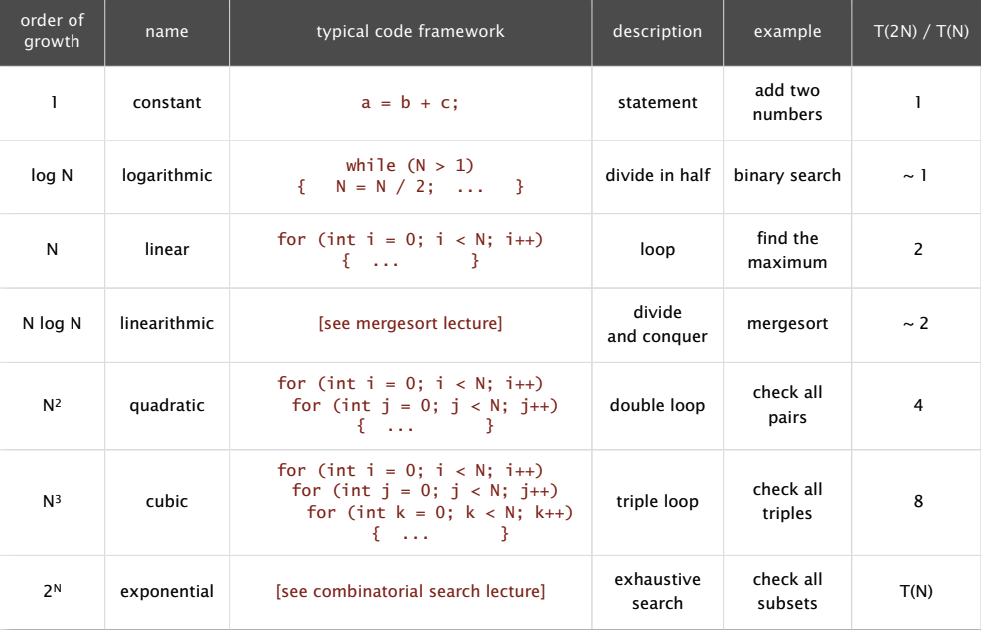
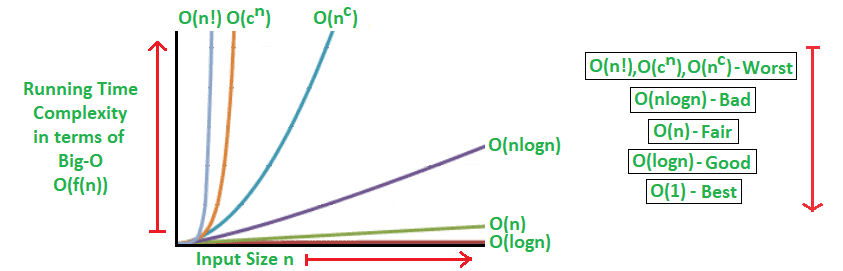
Ushbu jadvalda time complexity’larni best to worse tartibida ko’rib chiqamiz.