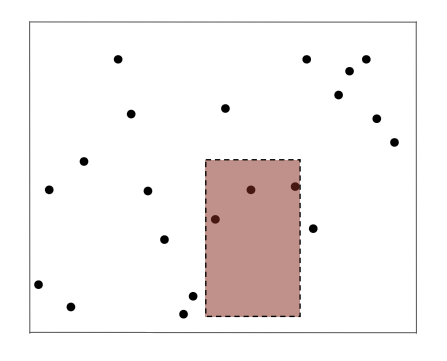
2D oraliq qidiruv (2D range search). 2D tree, KD tree

Masala. Berilgan kartadan ma’lum bir yuza ichiga kirgan nuqtalar sonini topish kerak. Ularni dasturda qanday qilib topamiz? Eng keraklisi, nuqtalarni dasturda qanday ifodalaymiz?

2D oraliq qidiruv. Image credit: algs4.cs.princeton.edu

Masalani samarali yechishning bir necha usullari bor:

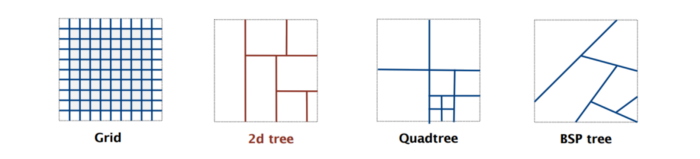
Grid. Kartani bir xil kattalikdagi kvadratlarga bo’lib chiqamiz.
2D tree. Rekursiya ichida ikkiga bo’lib chiqamiz.
Quadtree. Rekursiya ichida 4 ta kvadratga bo’lib chiqamiz.
BSP tree. Rekursiya ichida ikki regionga bo’lib chiqamiz.
KD tree. Rekursiya ichida K-o’lchamli kartani ikkiga bo’lib chiqamiz.

Kartani bo’laklarga ajratish turlari. Image credit: algs4.cs.princeton.edu

Yuqoridagi tree’lar Nearest Neighbor Search kabi boshqa masalalarni yechishda ham qo’l keladi.

Grid

Kartani (yoki yuzani) bir xil MxM hajmdagi kvadratlarga bo’lib olamiz. Kvadratlar katta ham, kichik ham bo’lib ketmasligi kerak.

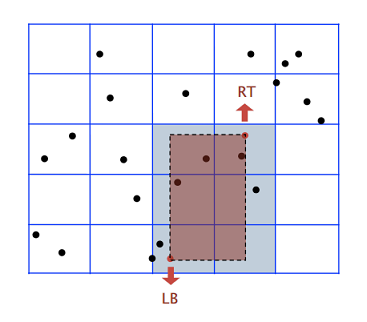
Har bir kvadrat ichidagi nuqtalarning ro’yxatini shakllantiramiz.
Har bir kvadratni indeksatsiya qilish uchun 2D array’ni ishlatamiz.
Qo’shishda yangi nuqtaning kooordinatasiga qarab u tushishi kerak bo’lgan kvadratni topamiz va nuqtani o’sha kvadratning ro’yhatiga qo’shamiz.
2D oraliq qidiruv (2D range search). Qidiruv shartiga qarab faqat kerakli kvadrat(lar) ro’yxati ichidan qidiruvni amalga oshiramiz.

Qidiruvning time complexity‘si O(1 + N/M²), ishlashda xotiradan O(M² + N) joy oladi.

Grid uslubi faqat nuqtalar kartada tarqalgan bo’lsagina samarali ishlaydi. Agar nuqtalar bitta kvadrat ichiga (klasterga) yig’ilgan bo’lsa, u holda berilgan oraliq yuzadagi nuqtalarni topish uchun bo’sh kvadratlarni ham tekshirib chiqishga to’g’ri keladi. Masalan biz quyidagi kartada faqat bitta klaster ichini qidirib oraliq yuzada joylashgan elementlarni tezda topishimiz mumkin edi.

Gridning yana bir muammosi – kvadratlarning o’lchamini topish, ya’ni kvadratlar o’lchami qanday bo’lganda qidiruv tezroq ishlashini aniqlash.

Agar kvadratlarni katta qilib olsak, griddagi bo’linishlar soni kamayadi, shunda qidiruvning samaradorligi kamayib ketadi. Chunki bitta kvadratda nuqtalar ko’payib ketgan bo’ladi.
Agar kvadratlarni kichkina qilib olsak, griddagi bo’linishlar soni ko’payib ketadi. Natijada biz ko’plab bo’sh kataklarga ega bo’lamiz.

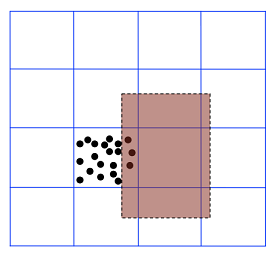
Quyidagi kartani olaylik:

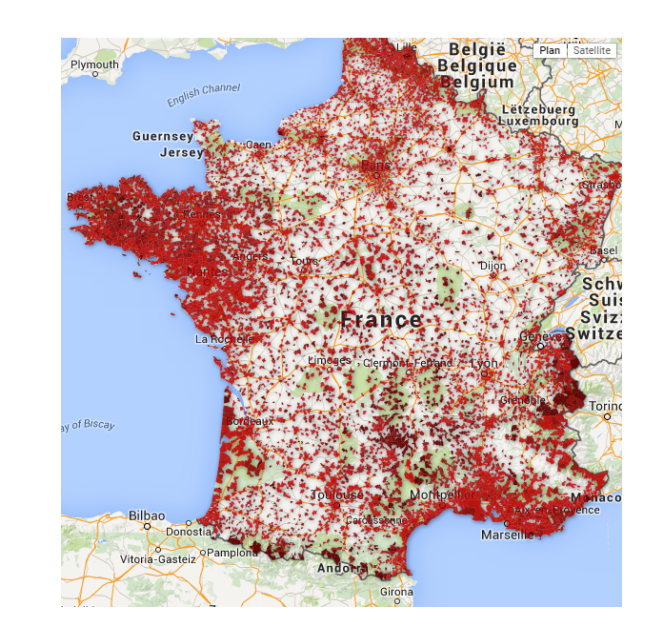
Kartani grid qilish samarasiz bo’ladi, chunki ko’rib turganingizdek, ba’zi joylarda nuqtalar o’ta zich joylashgan.

Xulosa qilib, kartani kataklarga bo’lib yuborish kam hollardagina samara berar ekan. Biz nuqtalarni karta yuzasi bo’yicha emas, soni bo’yicha bo’lib yuboramiz – 2D tree.

2D tree

Nuqtalarning soni bo’yicha bo’lish deganda, yuzada (kartada) nuqtalarning soniga qarab, ularning o’rtasidagi nuqtaga x yoki y o’qi bo’yicha chiziq tortish nazarda tutiladi. Bunda chiziqning ikki tarafida (deyarli) bir xil miqdordagi nuqtalar qolishi kerak.

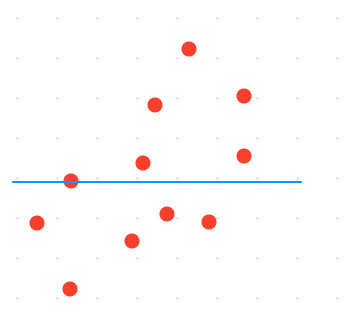
Yuzani nuqtalar bo’yicha o’rtadan bo’lish. Image credit: https://towardsdatascience.com/how-to-search-data-with-kdtree-aad5c82ebd99

So’ngra yarim yuzalarning ikki qismini ham nuqtalar soni bo’yicha ikkiga bo’lamiz.

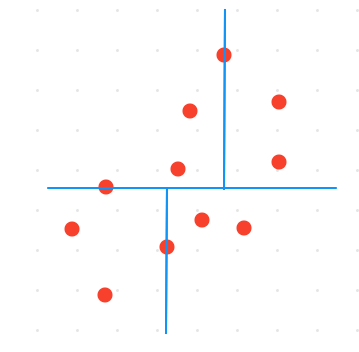
Bo’lishlarni rekursiv tarzda, bo’laklarda nuqta qolmaguncha yoki ma’lum bir sondagi nuqtalar qolguncha davom ettiramiz. Bo’lishlar dastlab y o’qiga perpendikulyar tarzda, keyin x o’qiga perpendikulyar tarzda, so’ngra y o’qiga, x o’qiga, y o’qiga… va hk ko’rinishida davom ettiriladi.

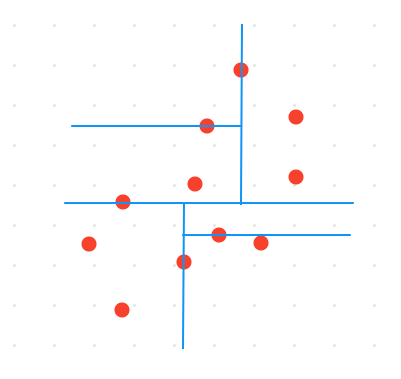
E’tibor bergan bo’lsangiz, bo’linishlar ierarxik tarzda davom etyapti. Demak biz bo’linishlarni tree ko’rinishiga keltirib olishimiz mumkin.

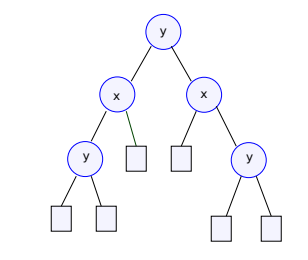
*Yuzadagi nuqtalarni tree’da ifodalash. Image credit:* https://towardsdatascience.com/how-to-search-data-with-kdtree-aad5c82ebd99

Yuzadagi nuqtalar asosida hosil bo’lgan tree – 2D tree deyiladi.

2D tree ko’rinishidan binary search tree‘ga o’xshaydi. Ammo farqli jihatlari mavjud:

Dastlab nuqtalar y o’qiga perpendikulyar tarzda (gorizontal chiziq) bo’lingani uchun, root node’ning key’i – y bo’ladi.
Uning ikki child’i x o’qiga perpendikular (vertikal chiziq) bo’lingani uchun – x ga teng.
Parent key’ning qiymati o’ng yoki chap child’lari key qiymatiga aloqasi yo’q (binary search’da parent key chap child’dan katta, o’ng child’dan kichik bo’lardi).

Nuqtalarni sonlar yordamida ifodalab olsak, 2D tree yasash ancha tushunarli ko’rinishga keladi.

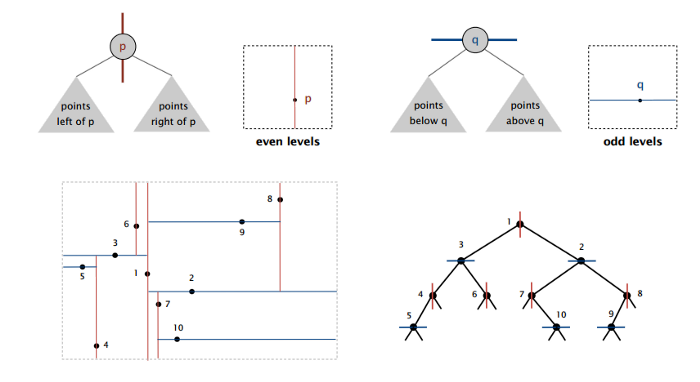
2d Tree Implementation— algs4.cs.princeton.edu

2D oraliq qidiruv

Berilgan yuza ichidan ma’lumot qidirish deganda 2D tree ichidan berilgan yuza ichidagi nuqtalarni topish tushuniladi. Qidirish rekursiya ichida, quyidagicha amalga oshiriladi:

Agar tekshirilayotgan nuqta (node) qidirilayotgan yuza (to’g’ri to’rtburchak) ichida yotgan bo’lsa, uni javoblar ro’yxatiga qo’shiladi.
Agar yuza tekshirilayotgan nuqtaning chap yoki past tarafida bo’lsa, qidiruvni 2D tree’ning chap child’idan davom ettiriladi.
Agar yuza tekshirilayotgan nuqtaning o’ng yoki yuqori tarafida bo’lsa, qidiruv 2D tree’ning o’ng tarafidan davom ettiriladi.

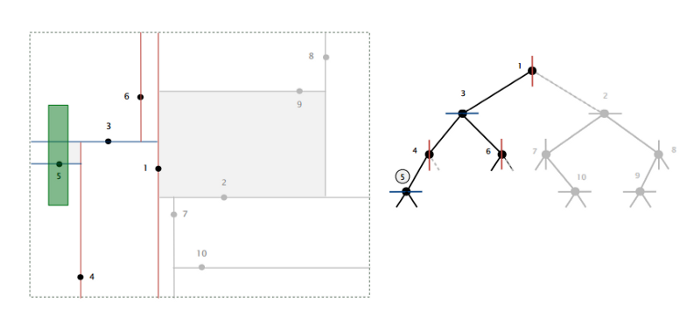
Range search in 2d tree — algs4.cs.princeton.edu

2D tree’da qidiruv o’rtacha O(R + log N), yomon holatda (worst case) – O(R + sqrt(N)) vaqtni oladi.

KD tree

Yuzalarni nuqtalar soni bo’yicha bo’lish amaliyotini 2D tree misolida ko’rib chiqdik. Huddi shu amaliyot KD tree uchun ham mos keladi. K bu yerda ko’rilayotgan yuzaning o’lchami. U 2 yoki 3 bo’lsa, 2D tree yoki 3D tree deb ham nomlanadi.

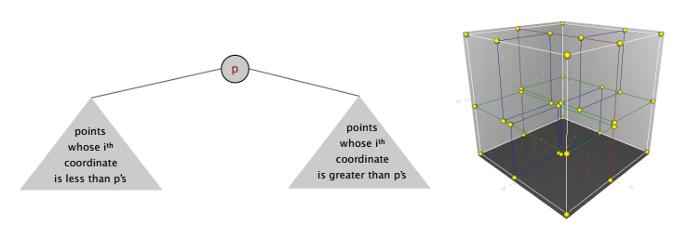
Kod

Hozircha KD-tree APIsida berilgan nuqtalardan KD-tree yasash, 2D tree uchun berilgan nuqtaga yaqin nuqtani topish (search nearest path) va to’g’ri to’rtburchak ichidagi nuqtalarni topish (2D range search) funksiyalari qo’shilgan.

* * *

Kod Githubda: https://github.com/Webmaxor/leetcode-solutions/blob/master/algorithms/trees/kd-trees.js

* * *

Mavzu bo’yicha savollarni Github’dagi Webmaxor / leetcode-solutions repository’da yozishingiz yoki kodda Reference in new issue ni bosib, qoldirishingiz mumkin.