Geometriyada Convex hull – barcha nuqtalarni (yoki obyektlarni) o’z ichiga olgan yuza perimetri yoki barcha tashqi nuqtalar ro’yhati.
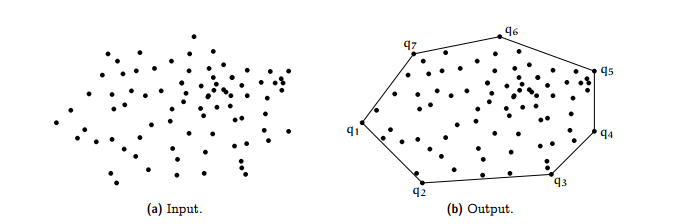
Convex hull uchun real hayotdan misol qilib, biror yuzada barcha daraxtlarni bog’lab turuvchi arqonni tasavvur qilamiz. Bog’langan arqon faqat tashqi tarafdagi daraxtlarga tegib turadi, yuzaning ichrog’ida joylashgan daraxtlar arqonga tegmaydi.
Convex hull’ni kodda ifodalash uchun odatda arqonga tegib turgan nuqtalar ro’yhati olinadi, ya’ni convex hull’ning nuqtalari ro’yhati topiladi.
Convex hull’ni topish
Nuqtalarning joylashuviga qarab inson ko’zi bilan tez orada qaysi nuqtalar convex hull’ga tegishli bo’lishini, ya’ni qaysi nuqtalar o’raladigan arqonga tegib turishini aniqlab oladi. Ammo bu intuitsiyani kodga o’zgartirish biroz vaqt talab qiladi.
Dasturda foydalanish uchun Convex hull nuqtalari ikki o’lchamli array ko’rinishida keladi. Masalan:
[[1,1], [2,2], [2,0], [2,4], [3,3], [4,2]]
Uni XY koordinatalar ko’rinishida tasavvur qilsak:
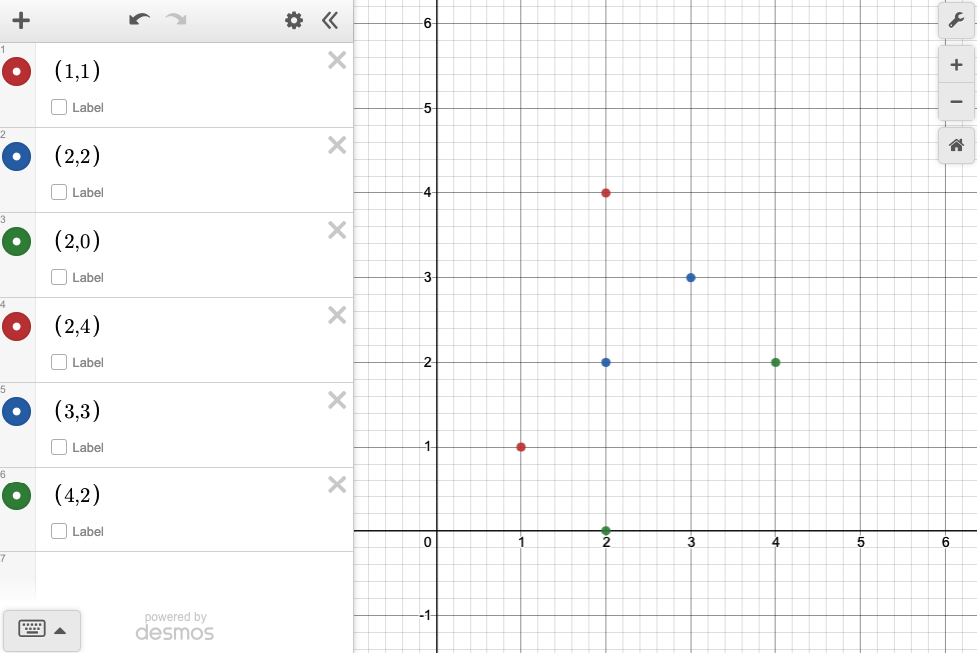
Koordinatalar bo’yicha xulosalar:
- [1,1] – X o’qi bo’yicha birinchi nuqta, [4,2] X o’qi bo’yicha ohirgi nuqta;
- [3,3] – [2,4] va [4,2] bilan bir chiziqda joylashgan;
- [2,2] – convex hull ichida, demak arqon bu nuqtaga tegmaydi.
Nuqtalarni arqon bilan o’rasak, quyidagicha yuza hosil bo’ladi:
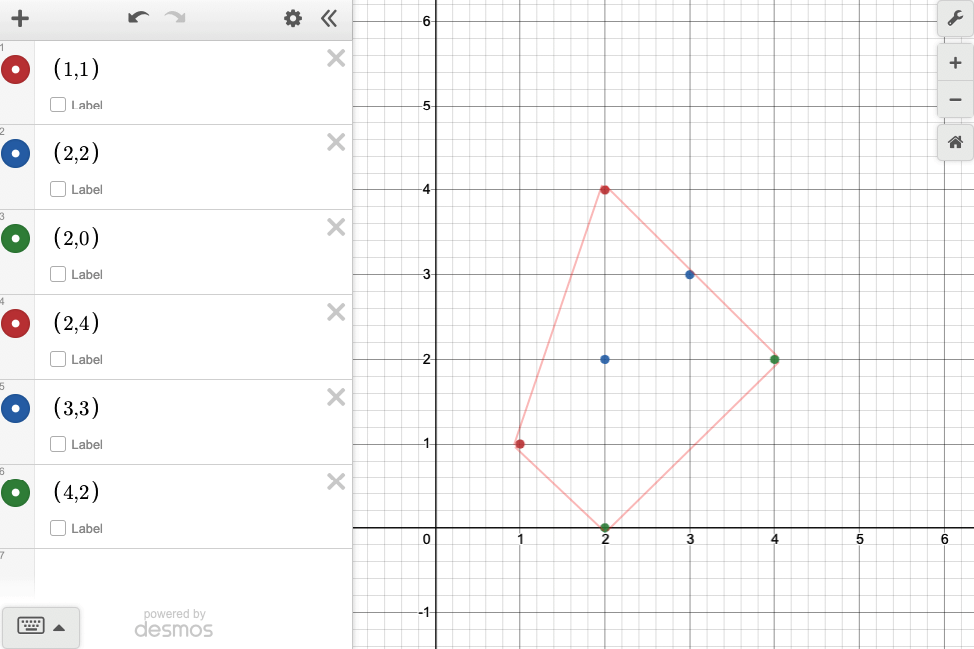
Convex hull nuqtalarini topish uchun, biz Monotone chain algoritmidan foydalanamiz. Algoritm X o’qi bo’yicha birinchi turgan nuqtadan boshlab, X o’qi bo’yicha ohirgi turgan nuqtagacha pastki nuqtalarni (lower hull) topib chiqadi. Keyin X o’qi bo’yicha ohirgi turgan nuqtadan boshlab, X o’qi bo’yicha birinchi turgan nuqtagacha yuqori nuqtalarni (upper hull) topib chiqadi. Upper hull yoki lower hull’dan qaysi birini birinchi bo’lib hisoblashning ahamiyati yo’q.
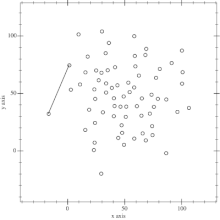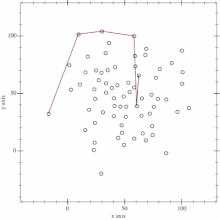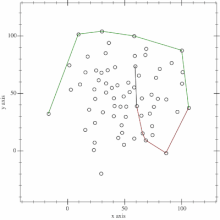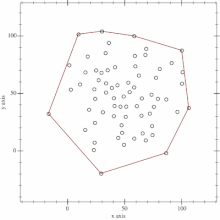
Algoritmga ko’ra, birinchi bosqichda nuqtalarni o’sish tartibida saralab olinadi. Saralash tartibi dastlab X o’qi bo’yicha, agar ikki X o’qidagi nuqta teng bo’lib qolsa, keyin Y o’qi bo’yicha bo’ladi. Bu degani – array’da dastlab, birinchi o’lchamni, keyin ikkinchi o’lchamni saralab olinadi. Kiritilgan input, saralash yakunlangach quyidagi ko’rinishda bo’ladi:
[[1,1], [2,0], [2,2], [2,4], [3,3], [4,2]]
Ikki nuqta – [2,2] va [2,0] o’rni almashdi. X o’qi nuqtalari teng bo’lgani uchun ([2,0], [2,2]), Y o’qi bo’yicha taqqoslandi ([2,0], [2,2]).
Algoritmdagi ikkinchi muhim jihat – uch nuqta o’rtasidagi yo’nalishni topish.
Yo’nalishlar uch turda bo’ladi:
- Soat strelkasi yo’nalishida
- Soat strelkasiga qarama-qarshi yo’nalishda
- Bir chiziqda
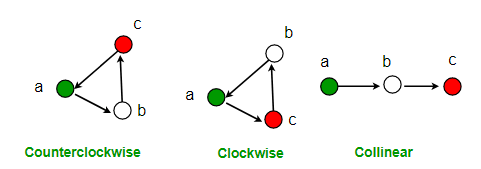
Yo’nalishni aniqlab olish formulasi:
- agar yo’nalish soat strelkasi bo’yicha bo’lsa, 0 dan katta son qaytaradi;
- strelkasiga qarama-qarshi bo’lsa 0 dan kichik son qaytaradi.
- bir chiziqda yotgan nuqtalar uchun 0 qaytaradi.
function orientation(p, q, r) {
return (q[1] - p[1]) * (r[0] - q[0]) - (q[0] - p[0]) * (r[1] - q[1])
}
Bizning tartiblangan inputda:
- dastlabki uch nuqta – [1,1], [2,0], [2,4] ga chiziq tortsak, chizishimiz soat strelkasi yo’nalishiga qarama-qarshi yo’nalishda bo’ladi. orientation() funksiya -4 qiymat qaytaradi
- [1,1], [2,4], [2,2] – soat strelkasi yo’nalishida – funksiya 2 qaytaradi.
- [2,4], [3,3], [4,2] – bir chiziqda – funksiya 0 qaytaradi.
Biz Monotone chain formulada dastlab lower hull, keyin upper hull’ni topishimiz bois, bizning yo’nalish soat strelkasiga qarama-qarshi bo’ladi. Shu tufayli, biz tartiblangan array’dan navbatma-navbat 3 ta nuqtani tekshirayotganimizda soat strelkasi yo’nalishi bo’yicha turgan ohirgi nuqtani tushirib qoldiramiz. Sababi bu nuqta yuzaning ichida joylashgan bo’ladi.
Nuqtalarni Stack-array’ga yig’amiz. Lower va upper hull nuqtalari topib bo’lingach, qaytarilgan (duplicate) nuqtalarni chiqarib tashlaymiz. Shunda bizda faqat arqon’ga tegib turgan nuqtalar qoladi.
Kod:
Kod Githubda: https://github.com/Webmaxor/leetcode-solutions/blob/master/problems/550-599/587.erect-and-fence.js
Yuqoridagi funksiya Leetcode’da 587. Erect and fence masalasi bo’yicha yozilgan, ammo istalgan 3 ta nuqta bo’yicha convex hull’ni topa oladi.
* * *
Mavzu bo’yicha savollarni Github’dagi Webmaxor / leetcode-solutions repository’da yozishingiz yoki kodda Reference in new issue ni bosib, qoldirishingiz mumkin.