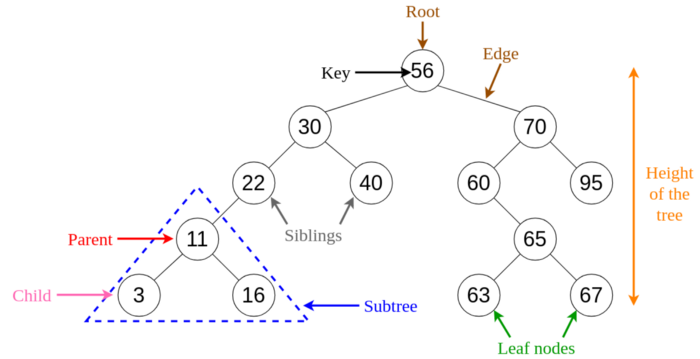
Binary search tree

Binary search tree (BST) – chap child’ining qiymati o’zidan kichik bo’lgan, o’ng child’ining qiymati o’zidan katta bo’lgan node’lardan iborat binary tree.

Mavzu: Tree ma’lumotlar tuzilmasi va binary tree

Binary search tree’ning binary heap’dan farqi – binary heap’da parent o’zining child’laridan katta bo’ladi, binary search’da esa parent chap child’dan katta va o’ng child’dan kichik bo’ladi.

BST ma’lumotlarni tezkor qidirish, qo’shish va o’chirish imkonini beradi. Elementlarni qidirish binary search prinsipi asosida bo’ladi: tree’dan elementni qidirishda (yoki yangi element qo’shishda), tree’ni root’idan leaf’gacha tushib keladi. Bunda har bir node’ga kelganda uni qidirilayotgan element bilan solishtirib, element katta bo’lsa, qidiruvni node’ning o’ng tarafidan; element kichik bo’lsa qidiruvni node’ning chap tarafidan davom ettiradi. Shu tariqa tree’dagi node’larning yarmidan ko’pi tekshirilmay tashlab ketiladi.

Agar tree – perfect binary tree bo’lsa, ishlash vaqti O(log N) gacha tushadi. N – tree’dagi node’lar soni.

Binary search tree da qidirish (search)

Quyidagi rasmda qidirish jarayonini tushunib olamiz:

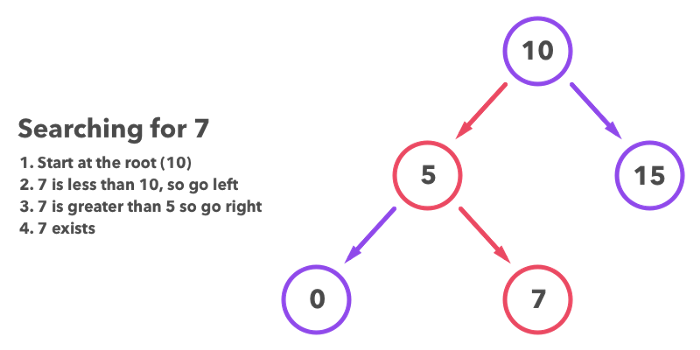
7 sonini BST dan qidiramiz.

Qidiruvni root (10) dan boshlaymiz.
7 < 10, root’ning chap tarafiga o’tamiz.
7 > 5, node’ning o’ng tarafida davom ettiramiz.
7 = 7, kerakli sonni topdik.

BST’ga ma’lumot qo’shish (insert)

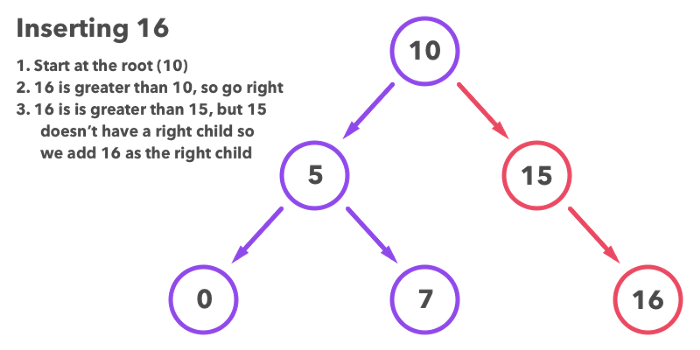
BST’ga ma’lumot qo’shish. Image credit: https://link.medium.com/oXl7cHounab

Ma’lumot qo’shishdan oldin uni BST’da qidiramiz. Agar mavjud bo’lsa, shunchaki uning qiymatini o’zgartiramiz. Yo’q bo’lsa, yangi child sifatida qo’shamiz.

BTS’ga 16 sonini qo’shamiz.

Qidiruvni root (10) dan boshlaymiz.
16 > 10, o’ng tarafga o’tamiz
16 > 15, lekin 15 ning child’i yo’q. Shu sababli 16ni 15 ning child’i sifatida qo’shamiz. 16 > 15 bo’lgani uchun, 16 o’ng tarafdagi child sifatida qo’shiladi.

BST’dan ma’lumot o’chirish (delete)

O’chirish jarayoni biroz murakkab, chunki biz tree’dan node’ni o’chirganimizdan keyin tree’ning butunligini saqlab qolishimiz ham kerak. Ya’ni node o’chirilgach, biz node’ning child’larini tekshirib, ularni kerakli parent’ga beramiz.

O’chirish 3 xil holatda bo’lishi mumkin

O’chirilayotgan node – leaf. Uni shunchaki o’chirish bilan qutilamiz.

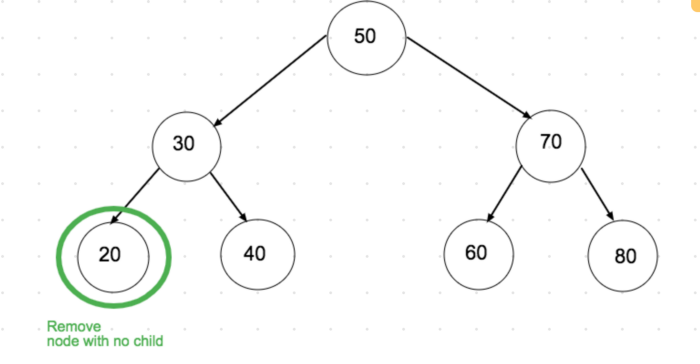
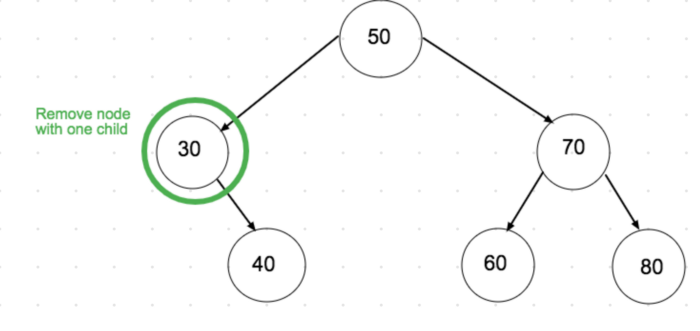
Child’i yo’q node’ni o’chirish. Image credit: https://levelup.gitconnected.com/deletion-in-binary-search-tree-with-javascript-fded82e1791c

O’chirilayotgan node’ning bitta child’i bor. Bunisi ham oson, node’ning child’ini uning parent’iga beramiz.

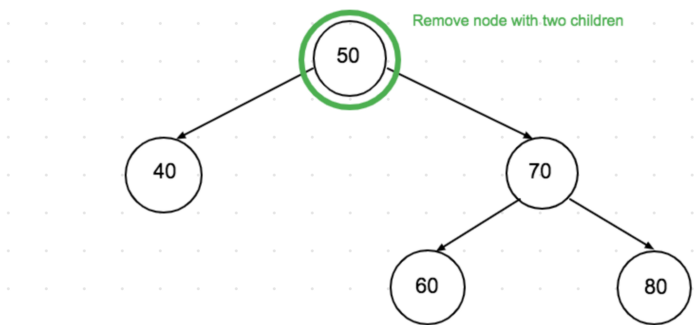
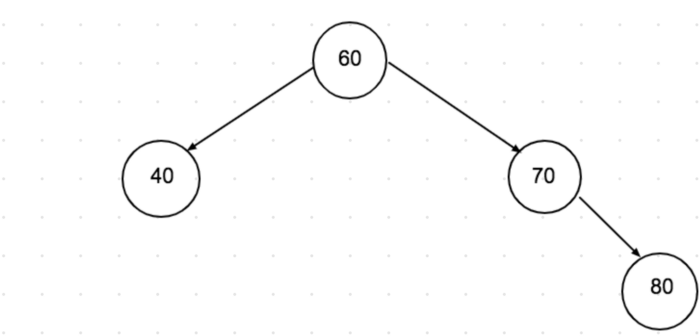
Bitta child’i bor node’ni o’chirish: *Image credit:* https://levelup.gitconnected.com/deletion-in-binary-search-tree-with-javascript-fded82e1791c

O’chirilayotgan node’ning ikki child’i bor. Murakkab qismi. Dastlab, o’chirilayotgan node’ning child’lari ichidan keyingi qiymatdagi node’ni topamiz. Keyin uning qiymatini o’chirilayotgan node’ga beramiz va keyin qiymatdagi node’ni tree’dan o’chiramiz.

Ikki child’i bor node’ni o’chirish. *Image credit:* https://levelup.gitconnected.com/deletion-in-binary-search-tree-with-javascript-fded82e1791c

O’chirish yakunlangach

Tree ikki child’i bor node o’chirilganidan so’ng. *Image credit:* https://levelup.gitconnected.com/deletion-in-binary-search-tree-with-javascript-fded82e1791c

Binary search’ning vizualizatsiyasini o’zingiz bu yerda sinab ko’rishingiz mumkin: https://www.cs.usfca.edu/~galles/visualization/BST.html

Binary search tree’ni array’da ifodalash

Binary search tree’ni array’da ifodalash mumkin. Muammo – agar binary tree perfect bo’lmasa, array’dagi ba’zi indekslar bo’sh qolib ketadi. Masalan quyidagi binary tree’ni array’da ifodalaymiz.

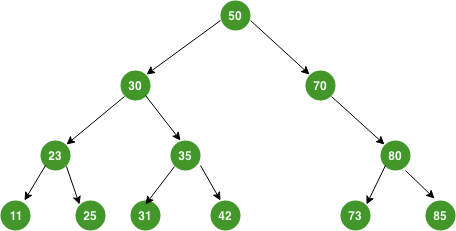
Hisoblashda oson bo’lishi uchun array[0] ni bo’sh qoldiramiz. array[1] – root; array[2] va array[3] root’ning ikki child’i bo’ladi.

[null, 50, 30, 70, 23, 35, 80, 11, 25, 31, 42, 73, 85]

Binary heap’dagi kabi parent’ning child’ini 2*i va 2*i + 1 topish mumkin. Bunda i – parent’ning indeksi.

Ok, hayot har doim ham bir tekis davom etmaydi. Tree kamdan-kam holatda perfect bo’ladi.

Yuqoridagi tree perfect emas, shu sabab uni array’da ifodalashda array’ning ba’zi indekslarida null qiymat paydo bo’ladi:

[null, 56, 30, 70, 22, 40, 60, 95, 11, null, null, null, null, 65, null, null, 3, 16, null, null, null, null, null, null, null, null, 63, 67, null, null, null, null]

Eng yomon holatdagi tree – degenerate search tree’ni ko’rib chiqamiz.

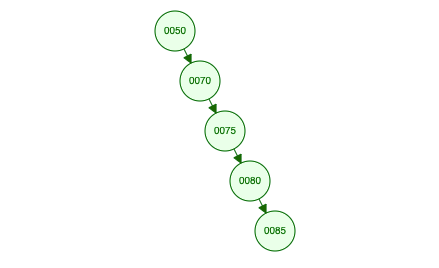
[null, 50, null, 70, null, null, null, 75, null, null, null, null, null, null, null, 80, null, null, null, null, null, null, null, null, null, null, null, null, null, null, null, 85]

5 ta elementdagi degenerate tree’ni ifodalash uchun array’da 31 da indeks band qilinyapti. Juda ham samarasiz.

Xulosa. Binary search tree faqat perfect bo’lgandagina, uni array’da ifodalashdan ma’no bor.

Linked list’da ifodalash

Linked list ma’lumot tuzilmasi tree’larni ifodalash uchun mos keladi. Tree turiga qarab linked list’dagi node’larning pointerlari bitta yoki undan ko’p bo’lishi mumkin. Biz binary search tree’ni linked list’da ifodalashni ko’rib chiqamiz.

Binary search tree’dagi har bir node’ning maksimum ikki child’i bo’lishi ehtimoli borligi uchun, Linked list’dagi node’ning ham ikki pointeri bo’ladi.

Mavzuning davomi va kod bu yerda: Binary search tree ustida amallar. API yozish