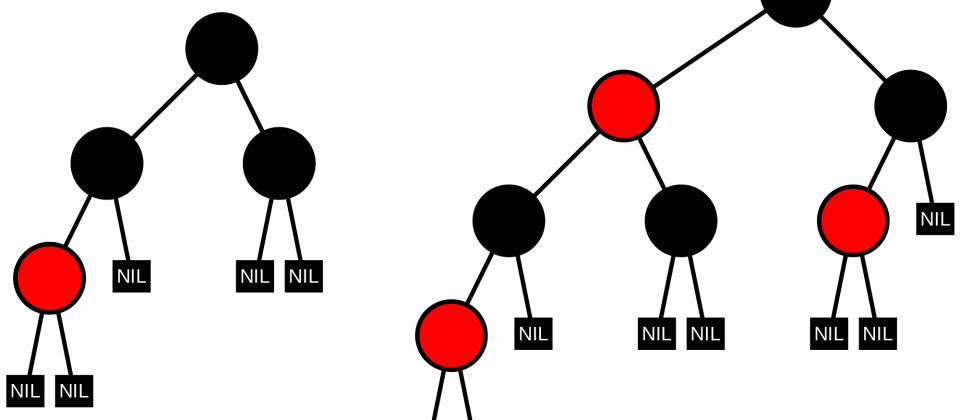
2-3 tree haqida tanishib chiqqan bo’lsangiz, unda node qo’shishda ko’p shartlarni hisobga olish kerak bo’lardi. Umuman, 2-3 tree’ni kodda ifodalash qiyin edi. Red-black tree mana shu insertdagi qiyinchiliklarga yechim sifatida keladi.
Red-black tree ham aslida 2-3 tree, lekin unda 3-node chap tarafdagi qizil bog’lanish bilan ajratiladi. Qizil chiziqli bog’lanish sababli Red-black tree binary search tree‘ga o’xshab qoladi.
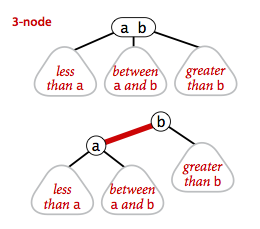
Shu yo’l bilan biz 2-3 tree ustida amallarni bajarish uchun kod yoza olamiz. Va albatta, binary search tree’ning API’sidagi ko’p amallar ham red-black tree’da ishlaydi.
2-3 tree’ni red-black tree’da ifodalash:
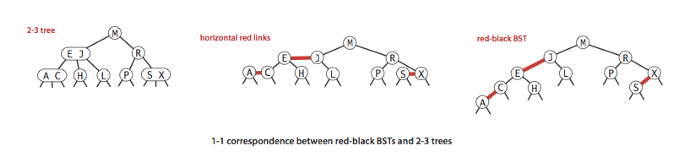
Red-black tree hususiyatlari
- Qizil bog’lanishlar 3-node’lar uchun yelim vazifasini o’taydi.
- Node’da ikki qizil bog’lanish bo’lishi mumkin emas, bu holda 4-node bo’lib qoladi va 2-3 tree’dagi kabi u uchta 2-node’ga ajratiladi.
- root’dan leaf’gacha barcha yo’nalishlarda bir xil sonda qora bog’lanishlar (odatiy bog’lanishlar) bo’ladi – ya’ni mukammal qora balansga ega.
- 3-node’ning katta qiymati parent’ga o’tadi, shu sababli qizil bog’lanish node’ning faqat chap tarafida bo’ladi (Biz faqat chap taraflama – Left leaning red-black tree‘ni ko’rib chiqamiz).
Red-black tree ustida amallar
Aynan red-black tree’ga tegishli bo’lgan amallar uchta, ularning barchasi qizil bog’lanishni chap tarafga o’tkazish yoki ikki qizil bog’lanish bo’lgan holatda ularni qora bog’lanishga o’zgartirishga xizmat qiladi.
Chapga burish (Rotate left).
Ba’zi amallardan keyin qizil bog’lanish node’ning o’ng tarafida bo’lib qoladi. Shunda tree’ni to’g’rilash uchun qizil bog’lanishni chap tarafga o’tkazishimiz kerak bo’ladi. Chapga burish deganda 3-node’ning ikkinchi qiymatini parent’ga o’tkazish tushuniladi. Quyidagi rasmda tushuntirishga harakat qilaman.
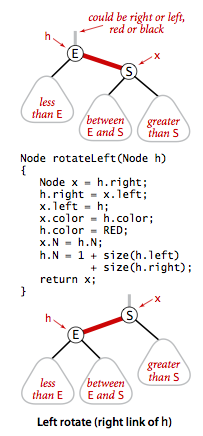
3-node (E S) da E parent bo’lib turipti va S uning o’ng tarafiga bog’langan. Biz S ni parent qilib olamiz. Shunda E qiymat S ning chap child’i bo’ladi va qizil bog’lanish chapga o’tadi. S parentning oldingi chap child’i E’ning o’ng child’iga o’tadi.
O’ngga burish (Rotate right)
Tree’ga element qo’shilgandan so’ng, ba’zi hollarda 3-node 4-node’ga aylanib, qizil bog’lanishli chap tarafdagi ketma-ket ikki node ko’rinishiga kelib qoladi.
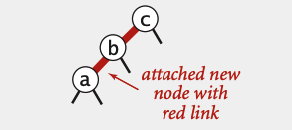
Uni to’g’rilash uchun 4-node o’ngga buriladi va B ikki tarafida qizil bog’lanishli parent’ga aylanadi. Keyin ikki qizil chiziq qoraga o’zgartiriladi, ya’ni 4-node B parent bo’lgan 3 ta 2-node’ga ajratiladi.
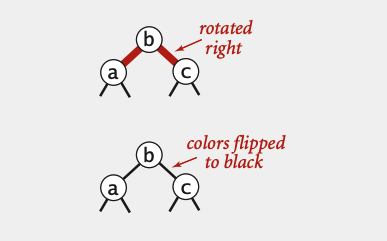
Qayd etish kerakki, o’ngga burish faqatgina eng katta qiymati parent bo’lgan 4-node uchun amal qiladi. Boshqa holatlarda o’ngga burishning hojati bo’lmaydi.
Rangni o’zgartirish (Color flip)
O’ngga burish misolida ko’rganimiz, node’ning ikki tarafida qizil bog’lanish bo’lib qolganda uning rangi qoraga o’zgartiriladi. 2-3 tree qoidasi bo’yicha 4-node 3 ta 2-node’ga ajratiladi.
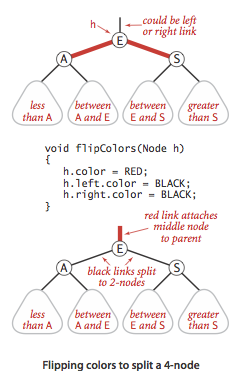
Yuqoridagi amallardan red-black tree’ni simmetrik tartibda, mukammal balansda ushlab turish, shuningdek 2-3 tree bilan bir xil ko’rinishda qoldirish uchun foydalaniladi.
Qo’shish (Insert)
Binary search tree kabi, element qo’shishdan oldin u red-black tree’da qidiriladi. Topilmasa, yangi element tree’ga qo’shiladi. Qo’shishning birnecha shakli mavjud:
2-node’ga qo’shish. Element shunchaki 2-node’ga qo’shiladi va u 3-node’ga aylanadi. Agar qizil bog’lanish o’ng tarafda bo’lib qolsa, 3-node chapga buriladi (katta elementi parent bo’ladi).
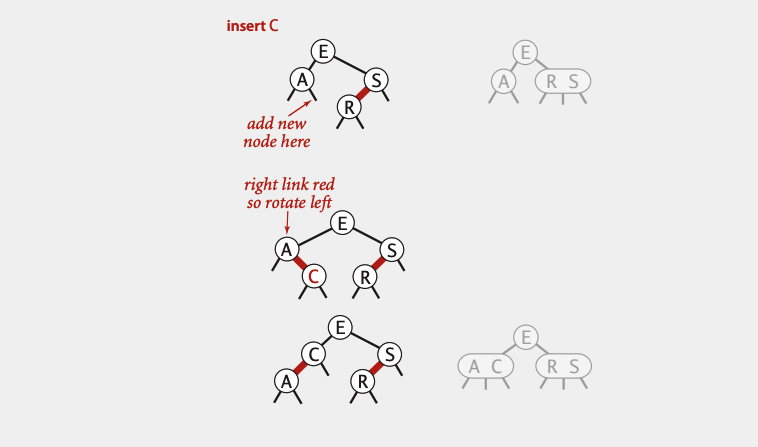
3-node’ga qo’shish.
- Qo’shilayotgan element parent’dan katta bo’lsa, o’ng child sifatida qo’shiladi. 3-node 4-node’ga aylanib qolgani uchun qizil bog’lanishlar qoraga o’zgaradi.
- Qo’shilayotgan element parentdan kichik bo’lsa, u chap child sifatida qo’shiladi. 4-node’ga aylanib qolgani uchun, o’ngga buriladi va qizil bog’lanish qoraga o’zgaradi.
- Qo’shilayotgan element 3-node’ning ikki elementi orasida bo’lsa, kichik elementning o’ng child’i bo’lib qo’shiladi. O’ng qizil bog’lanishni yo’qotish uchun pastdan birinchi va ikkinchi node’lar chapga buriladi, so’ng parent’i o’ngga buriladi. Ohirida ikki qizil bog’lanish qoraga o’zgaradi.
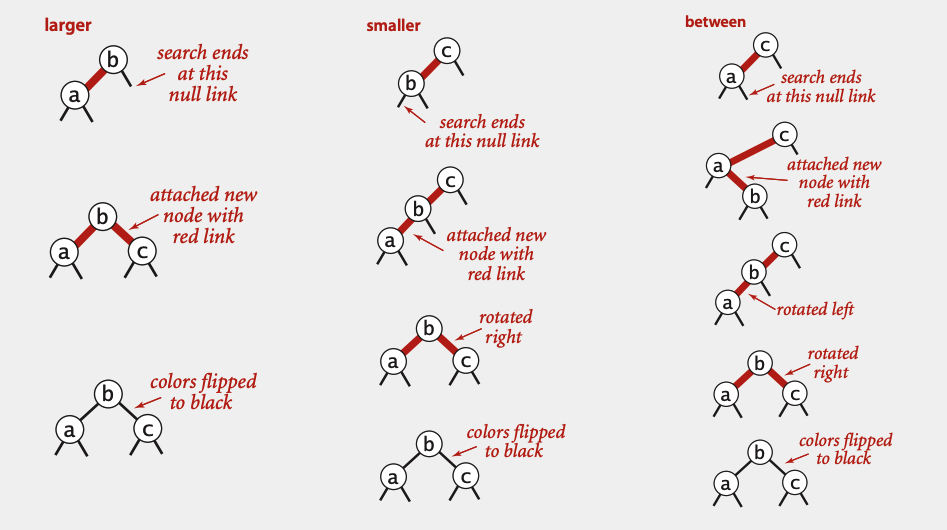
Qo’shish shakllarini umumlashtiradigan bo’lsak:
- O’ng child qizil bog’lanishda: chapga buriladi.
- Chap child va uning chap childi qizil bog’lanishda: o’ngga buriladi.
- Ikki child qizil bog’lanishda: qizil bog’lanish qoraga o’zgaradi.
O’chirish (Delete)
O’chirish qiyin bo’lgani uchun, to’xtalib o’tirmadim. Binary search tree’dagi delete funksiyasi ham red-black tree uchun ishlaydi ammo bunda daraxtning uzunligi ortadi.
Tahlil
Boshqa tree’larda bo’lgani kabi, ishlash vaqti daraxtning uzunligiga teng. Red-black tree deyarli mukammal balansga ega bo’lgani uchun, time complexity kafolatlangan O(log N).
- eng yomon holatda – root’dan leaf’gacha yo’lda qizil va qora bog’lanishlar bir xil sonda bo’lganda tree uzunligi ikki baravar oshadi. Uzunlik ≤ (2 LogN) bo’ladi.
- o’rtacha holatda daraxt uzunligi ~ 1.00 Log N (1.00 – 1 dan kattaroq son, lekin 1 ga juda yaqin).
- eng yaxshi holatda – daraxt mukammal balansga ega bo’lsa, daraxt uzunligi Log N ga teng bo’ladi.
* * *
Red-black tree ustida amallar uchun API yozish – bu yerda.