1D interval search (1D interval qidiruv) deb berilgan interval asosida u bilan kesishadigan boshqa intervallarni topishga aytiladi.
Biz 1D interval search’ni interval search tree yordamida ifodalash va tree’da qidirishni ko’rib chiqamiz.
Interval search tree
Interval search tree – binary search tree strukturasi yordamida yasaladigan ma’lumot tuzilmasi. Amaliyotda ishlash samaradorligini oshirish uchun red-black tree‘dan foydalaniladi. Har bir node’da 2 ta key – intervalning boshi (yoki pasti, low) va ohirgi (yoki yuqorisi, high) qiymatlari bo’ladi. low qiymatidan node’ning key’i sifatida foydalaniladi. Shuningdek node’da node child’laridagi eng katta high intervalining qiymati ham saqlanadi.
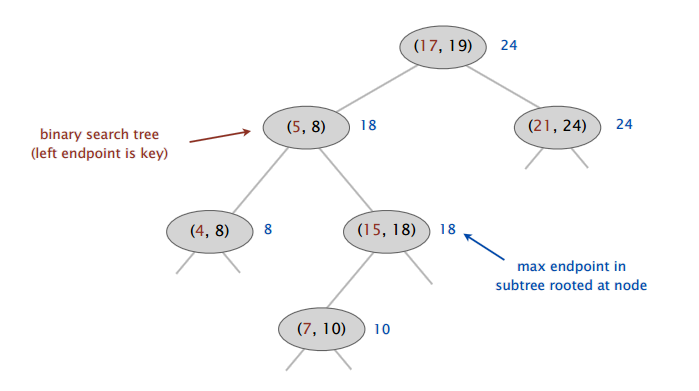
Interval search tree’da low qiymatlar key sifatida ishlatilayotgani uchun tree’da bir xil low qiymatli intervallarni saqlay olmaymiz. Sababi – tree’dagi key’lar unikal bo’lishi kerak.
Tree’ga interval qo’shish binary search tree kabi bo’ladi. Biz dastlab low qiymatlar bo’yicha qidirib qo’shilishi kerak bo’lgan joyni topamiz. Keyin root’gacha orqaga qaytib, yo’ldagi har bir node’da maksimum high interval qiymatini solishtirib, kerak bo’lganda yangilaymiz. Orqaga qaytish bor bo’lgani uchun, qo’shishda rekursiv funksiya ishlatiladi.
1D interval search amalining ishlashi quyidagicha:
- Agar tekshirilayotgan node’ning intervali berilgan interval bilan kesishsa, uni qaytaradi. Ish tugaydi.
- Agar chap sub-tree bo’sh bo’lsa, o’ng sub-tree’dan tekshirishni davom ettiradi.
- Agar chap sub-tree’dagi max high qiymat, berilgan intervalning low’idan kichkina bo’lsa, o’ng sub-tree’dan tekshirishni davom ettiradi.
- Aks holda chapdan davom ettiradi.
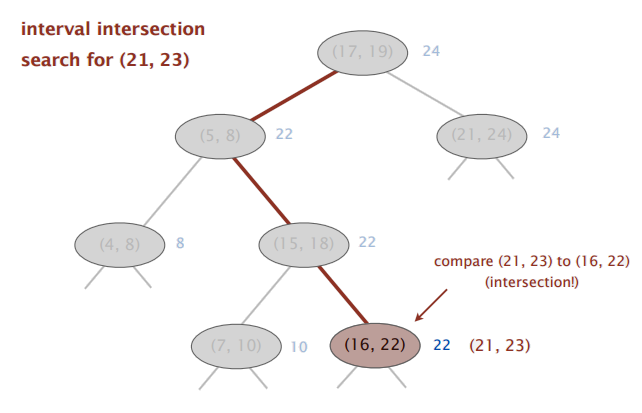
Kesishuvning (intersection) ikki holati mavjud. Birinchi holatda, agar biz o’ng sub-tree’ga o’tadigan bo’lsak, demakki chap sub-tree’da kesishuv yo’q bo’ladi. Isboti sifatida biz low qiymatni chap sub-tree’dagi max qiymat bilan tekshirganimizni keltiramiz.
Ikkinchi holatda, agar biz chapga o’tsak, demak chapda intersection bor yoki intersection umuman yo’q. Isboti – berilgan intervalning high qiymati chap sub-tree’dagi eng kichik node’ning low qiymatidan kichik bo’lishi.
Ushbu algoritm hamma kesishuvlarni topmaydi, faqat bitta interval topilishi bilan ishni tugatadi. Masalan yuqoridagi rasmda chap tarafda ham [16, 22], o’ng tarafda ham [21, 24] kesishuv bor. Algoritm faqat bitta kesishuvni topadi xolos.
Ikki intervalning kesishuvini aniqlash
Agar solishtirilayotgan ikki interval uzunligining yig’indisi ularning minimum low va maksimum high nuqtalari uzunligidan katta bo’lsa, demak ikki interval kesishadi.
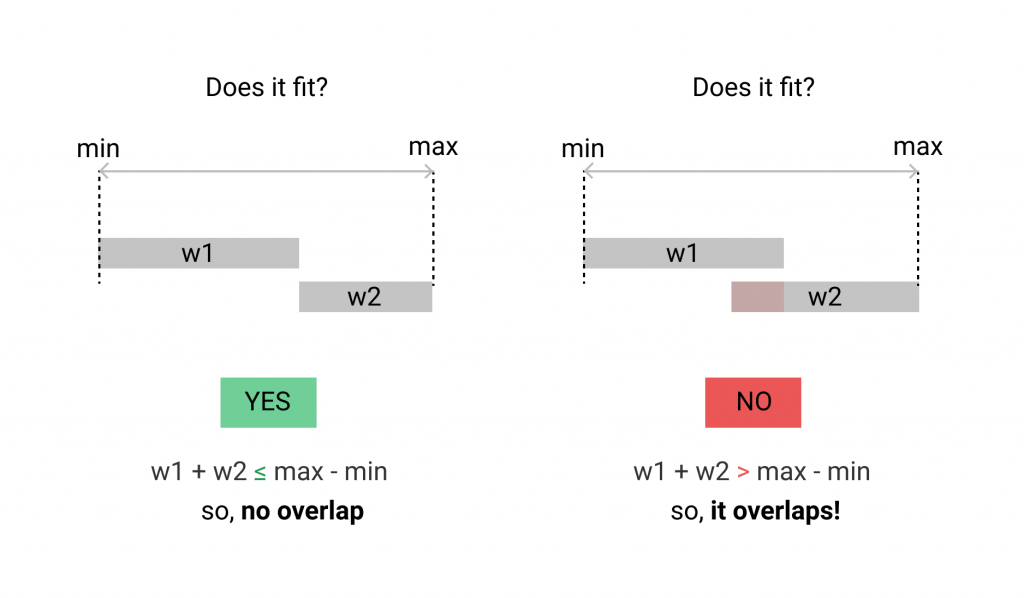
[a1, a2] va [b1, b2] intervallar uchun:
if (Math.max(a2, b2) - Math.min(a1, b1) < (a2 - a1) + (b2 - b1)) {
// ikki interval kesishadi
}
Tahlil
Qo’shish (insert) va bitta kesishgan intervalni qidirish (search) O(log N) vaqt oladi. Barcha kesishuvlarni topish esa – O(R log N), bu yerda R – kesishuvlar soni.
Kod
Interval search tree APIda tree yasash va tree’dan intervalni topish funksiyalari yozilgan.
Kod Githubda: https://github.com/Webmaxor/leetcode-solutions/blob/master/algorithms/trees/interval-search-trees.js
* * *
Mavzu bo’yicha savollarni Github’dagi Webmaxor / leetcode-solutions repository’da yozishingiz yoki kodda Reference in new issue ni bosib, qoldirishingiz mumkin.
