Graph ma’lumotlar tuzilmasini kodda ifodalashning bir necha usullari bor. Amaliyotda qo’yiladigan masalaga qarab usullardan biri tanlanadi.
Edge list
Edge list (yoki array) – E miqdordagi edge’larning oddiy ifodalanishi hisoblanadi. Bunda edge’lar array’da vertex juftlari bilan yoziladi. Misol uchun quyidagi graph’ni edge list’da ifodalash kerak bo’lsin.
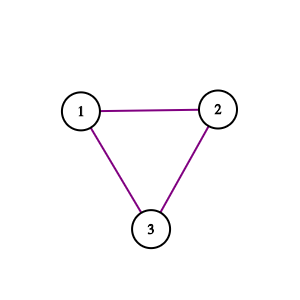
Biz har bir edge uchun vertex juftlarini array’ga kiritamiz:
[ [1, 2], [2, 3], [3, 1] ]
Oson, to’g’rimi? Ha, ammo osonlikning to’lovi bor.
Edge list’dagi qiymatlar tartiblanmagan. Biz bitta vertex’ning edge’larini topishimiz uchun barcha edge’larni tekshirib chiqishimiz kerak. Shunda edge list uchun time complexity – O(E) ga teng bo’ladi. Kichik graph’larda ishlash tezligi katta farq qilmaydi albatta. Lekin amaliyotda million, milliard edge’lari bo’lgan graph’larga duch kelamiz. Bunday holatda edge list bizga samaradorlikni taqdim eta olmaydi.
Edge list’ni directed va undirected graph’lar uchun birday ishlatish mumkin.
Undirected graph’larda edge’ni topish uchun barcha edge’larning ikki qiymatini (vertex’ini) tekshirish kerak bo’lsa, directed graph’larda bitta tekshirish yetarli bo’ladi.
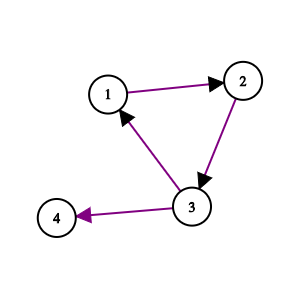
[ [1, 2], [2, 3], [3, 1], [3, 4] ]
3 ning edge’larini topish uchun edge’ning birinchi qiymati 3 ga teng bo’lgan barcha edge’larni olamiz: [3, 1] va [3, 4] . Agar berilgan edge’lar avvaldan tartiblanmagan bo’lsa, demak ishlash vaqti o’zgarmasdan qoladi. Birinchi vertex’lari qiymati bo’yicha tartiblangan directed graph’ning edge list’i uchun esa binary search‘ni qo’llab ko’rish mumkin.
Adjacency matrix
Adjacency matrix – graph’dagi qaysi vertex’larda bog’lanishlar (edge’lar) borligini ifodalovchi matritsa. Matritsaning eni va bo’yida vertex’lar, matritsa yacheykalarida esa ularning bog’lanishlari saqlanadi. Agar bog’lanish bo’lsa, 1 aks holda 0 ifodalanadi. Biz yuqorida ko’rib o’tganimiz (1, 2,3) vertex’dan iborat undirected graph’ni Adjacency matrix’da ifodalasak:
| 1 | 2 | 3 | - - - - - - - - 1 | 0 | 1 | 1 | - - - - - - - - 2 | 1 | 0 | 1 | - - - - - - - - 3 | 1 | 1 | 0 |
Adjacency matrix’ning ba’zi foydali hususiyatlari bor:
- Agar matritsada ichki bog’lanish (self edge) bo’lmasa, u holda matritsaning diagonali 0 lardan iborat bo’ladi.
- Undirected graph uchun matritsaning diagonali simmetrik bo’ladi, ya’ni diagonalning pasti va yuqori qismi bir biriga teng.
- Matritsaga qarab graph’ni directed yoki undirected ekanligini aytib berish mumkin.
- Matritsaga edge qo’shish yoki edge o’chirish O(1) vaqt oladi, chunki biz edge qo’shish uchun ikki vertex’ning qiymatini bilganimiz sababli, matritsadan vertex’larni qidirib o’tirishimiz shart bo’lmaydi.
Endi directed graph’ni adjacency matrix’da ifodalasak
| 1 | 2 | 3 | 4 | - - - - - - - - - - 1 | 0 | 1 | 0 | 0 | - - - - - - - - - - 2 | 0 | 0 | 1 | 0 | - - - - - - - - - - 3 | 1 | 0 | 0 | 1 | - - - - - - - - - - 4 | 0 | 0 | 0 | 0 |
Adjacency list’ning ham to’lovi bor.
V sonli vertex’larga ega graph’ni ifodalash uchun O(V2) miqdorda xotiradan joy kerak. Agar graph’da edge’lar soni vertex’lar sonidan ancha ko’p bo’lsa, ya’ni graph zich (dense) bo’lsa, matritsa usuli yomon emas. Graph’da edge’lar kam bo’lganda – siyrak (sparse) holatida, 0 lar bilan to’ldirilgan, ammo joy isrof qiladigan samarasiz matritsaga ega bo’lamiz.
Adjacency list
Adjacency list – edge list va adjacency matrix’ning gibrid ko’rinishi bo’lib, u linked list’lardan iborat array’ga ega. Array elementlari soni – V – graph’dagi vertex’lar soniga teng. Har bir elementdagi linked list esa vertex’ning edge’larini, yoki boshqacha aytganda, qo’shni vertex’larini ifodalaydi.
Yuqoridagi undirected graph’ni adjacency list’da ifodalasak:
[ 1 → 2 → 3, 2 → 3 → 1, 3 → 1 → 2]
→ = linked list’dagi pointer.
Directed graph uchun:
[ 1 → 2, 2 → 3, 3 → 1 → 4]
Adjacency list’da vertex’ni topish vaqti, agar vertex array index’ida ifodalangan bo’lsa – O(1) ga teng. Masalan graph’dan 3 vertex’ni topish uchun V[(3 – 1)] qilib murojaat qilamiz. Nima uchun 3 – 1? Sababi vertex’lar array’ning nolinchi elementidan boshlanayotgani uchun.
Vertex’ning barcha edge’larini topish vaqti ham O(1) ga teng. Eng yomon holatda esa O(d) ga. Bunda d – vertex’ning degree’si, vertex’ning edge’lari soni.
E’tibor bergan bo’lsangiz, directed va undirected graph’larni adjacency list’da ifodalashda har bir vertex’ning edge’lari soni farq qilmoqda. Undirected graph uchun vertex’lar soni 3, edge’lar soni 6 ta. Directed graph uchun vertex’lar soni 3 ta, edge’lar soni 4 ta. Agar vertex’lar sonini bir xil qoldirish uchun 4-vertex’ni olib tashlasak, edge’lar soni 3 ta qoladi. Bu degani, undirected graph’da ikki vertex o’zining edge’larini alohida-alohida ifodalayapti. Ya’ni undirected bo’lgani uchun bitta edge ikki vertex’da ham takrorlanyapti.
Xulosa qiladigan bo’lsak, undirected graph’ni adjacency list’da ifodalash directed graph’ga qaraganda 2*E baravar ko’p joy oladi. E – edge’lar soni.
API
Adjacent list uchun sodda API. Linked list o’rniga Set ishlatilgan. Set haqida bu yerda tushuntirilgan: https://walker.uz/2020/10/06/dictionary-yoki-symbol-table/
API keyingi mavzularga qarab, to’ldirib boriladi. O’zgarishlarni bu yerda kuzatib borishingiz mumkin: https://github.com/Webmaxor/leetcode-solutions/blob/master/algorithms/graphs/adjacency-list-graph.js
* * *
Manbalar:
https://medium.com/basecs/from-theory-to-practice-representing-graphs-cfd782c5be38
Graph editor: https://csacademy.com/app/graph_editor/