Graph ma’lumotlar tuzilmasi

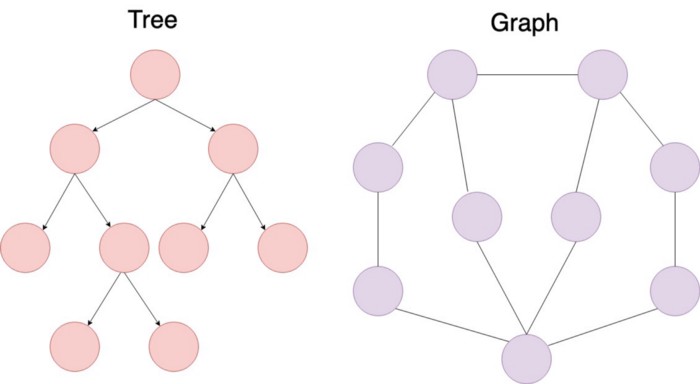
Biz chiziqli bo’lmagan ma’lumotlar tuzilmasini o’rganishni boshlaganimizda, ularning bazaviy xarakteristikasini ko’rib chiqqan edik: tuzilmadagi ma’lumotlar qandaydir tartibga ega emas (hech bo’lmaganda sanoq tartibiga ega emas). Masalan tree node’lari tartiblanmagan, node’lar faqat pointer orqali boshqa node’larga bog’lanishi mumkin. Tree’lar aniq bir qoidalarga bo’ysunadi. Bitta root node bo’ladi, uning child’lari bo’lmasligi yoki birnecha child’larga ulangan bo’lishi va hokazo. Ba’zi tree’lar o’ziga xos hususiyatlarga ega – binary search tree da faqat ikki bog’lanish va ularda bittadan node bo’lishi mumkin xolos.

Ok, tree‘dagi node’lar aniq qoidalar bo’yicha bir biriga bog’lanar ekan. Biz bog’lanish qoidalariga amal qilmasakchi? Masalan root tushunchasi bo’lmasa, hamma node’lar bir xil darajada bo’lsa, istalgan node’ni istalgan node’ga bog’lash imkoni bo’lsa… Buning imkoni bor albatta – graph ma’lumotlar tuzilmasi bilan.

Tree aslida graph’ning ma’lum bir cheklov va qoidalarga asoslangan varianti xolos. Qisqacha aytganda, istalgan tree bu graph, ammo istalgan graph tree emas.

Graph bu har bir node boshqa node’larga bog’langan (bog’lanishi mumkin bo’lgan) node’lar kolleksiyasi.

Graph’ning edge’lari (tomonlari) ikki turda bo’lishi mumkin:

1. Directed edges (yo’nalishli tomonlar) – node’lar o’rtasidagi bog’lanish bir tomonlama (unidirectional) bo’ladi. Birinchi node – yo’nalishning boshlanishi, ikkinchi node – manzil dib qaraladi.
2. Undirected edges (yo’nalishsiz tomonlar) – node’lar ikki taraflama bog’langan bo’ladi.

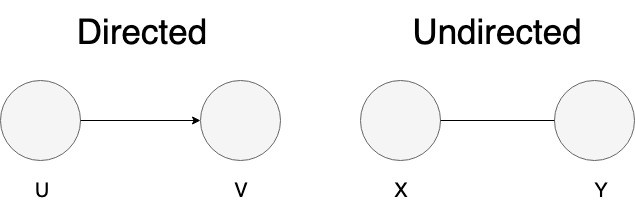
Odatda graph’lar edge’larning turiga qarab, directed graph va undirected graph ga ajratiladi. Ba’zan bir graph’da ikki turdagi edge’lar ham qatnashgan bo’lishi mumkin.

Graph atamalari

class GraphAtamalar extends TreeAtamalar 😉
Tree mavzusidagi atamalarning aksariyati graph’lar uchun ham qo’llaniladi. Qo’shimcha atamalarni quyida keltirib o’tamiz:

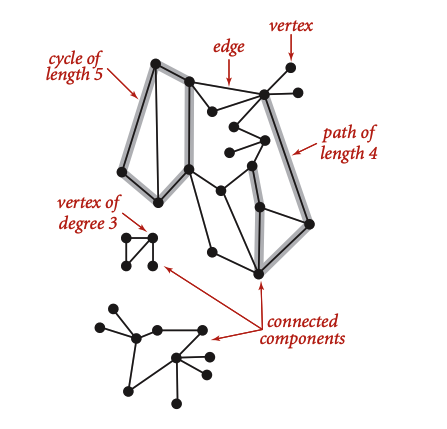
Vertex (yoki vertice, ko’plikda vertices) – node’ning o’zi. Node ko’proq amaliyotda qo’llaniladi, vertex nazariyada. Shuning uchun ham graph mavzularida vertex yoki vertice deganimizda node’ni tushunib olaverasiz.

Path – ikki va undan ko’p node’lar orasidagi yo’l. Path uzunligi soni path’dagi node’lar orasidagi edge’lar soniga teng bo’ladi.

Cycle – agar node’lar orasidagi yo’l (path) yopiq, aylana ko’rinishida bo’lsa, ya’ni yo’l boshlanish node’da tugasa, demak path – cycle bo’ladi. Cycle uzunligi soni ham path’dagi kabi node’lar orasidagi edge’lar soniga teng.

Degree (daraja) – node’ning boshqa node’larga bog’lanishlari soni. Agar node boshqa 3ta node’ga bog’langan bo’lsa, uning degree‘si 3 ga teng bo’ladi.

Graph qachon ishlatiladi?

Real hayotdagi juda ko’p tizimlar graph’larga asoslangan bo’ladi. Masalan Facebook ijtimoiy tarmog’idagi do’stlik aloqalari undirected graph’ga asoslangan. Siz Facebookdagi do’stingiz uchun ham do’st hisoblanasiz. Ya’ni do’stlik ikki tomonlama bog’langan.

Twitter va Instagram tarmoqlaridagi do’stlik (yoki kuzatish – follow) esa bir tomonlama bog’lanishga ega. Siz kuzatadigan odamlar sizni kuzatmasligi mumkin. Demak Twitter va Instagramdagi following – directed graph hisoblanadi.

Shuningdek, xaritalarni graphga aylantirish mumkin. chorrahalarni (ko’chalarning bog’lanishlarni) node deb oladigan bo’lsak, ko’chalarning o’zi edge bo’ladi. Kartani graph’ga aylantirgach, siz bir nuqtadan boshqasiga eng qisqa yo’lni hisoblash imkoniga ega bo’lasiz.

Boshqa misollar:

Weighted edges

Ko’chalar (yoki shaharlar) orasidan eng qisqa yo’lni tanlash misoliga to’xtaladigan bo’lsak, xaritani graph’larda ifodalashning o’zi qisqa yo’lni topish uchun kamlik qiladi. Sababi qisqa yo’lni topishga yana ko’chalarning uzunligi, ko’chadagi traffikning kamligi, ko’chadagi tezlikning cheklanganligi kabi faktorlar ham muhim rol o’ynaydi. Faktorlar asosida biz ko’chalarning afzalliklarini nisbiy sonlar bilan belgilab chiqamiz. Ushbu afzallik o’lchovi uchun weighted edges atamasi kiritilgan. Weight soni yuqori bo’lgan edge afzalroq edge deb baholanadi.

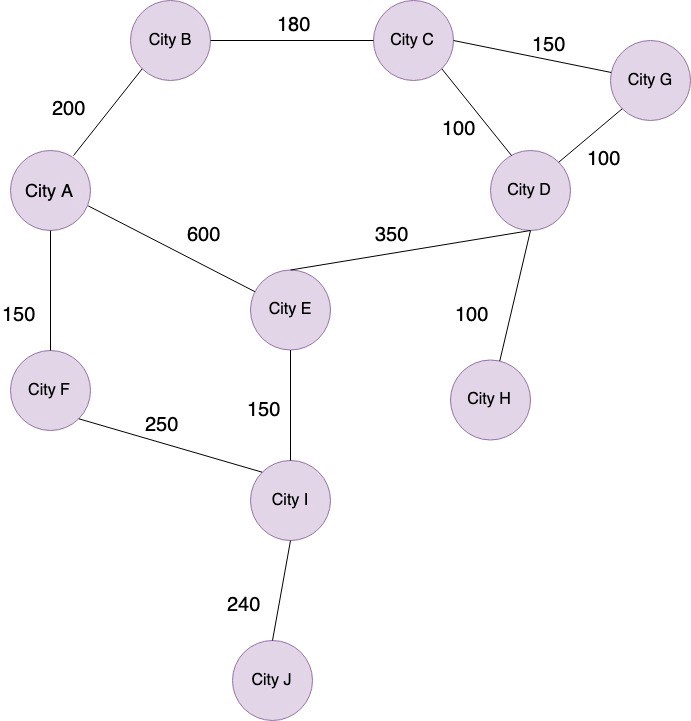
Yuqoridagi graph asosida A shahardan H shaharga yetib olish uchun eng qisqa yo’lni topish kerak bo’lsin. Biz A dan H gacha bo’lgan barcha path’larni edge’larning uzunligi bo’yicha hisoblab ko’ramiz.

1. A → B → C → D → H = 200 + 180 + 100 + 100 = 580
2. A → B → C → G → D → H = 200 + 180 + 100 + 150 + 100 = 730
3. A → E → D → H = 600 + 350 + 100 = 1050
4. A → F→ I → E → D → H = 150 + 250 + 150 + 350 + 100 = 1000

Uchinchi path’ning umumiy soni 1050, demak bu path boshqa path’lardan afzalroq ekan.

Graph traversal

Albatta biz graph’lar ichidan qisqa (yoki afzal) path’ni topish uchun qo’lda hisoblab o’tirmaymiz. Ayniqsa katta graph’lar uchun hisoblashlar inson uchun ko’p vaqt talab qiladi. Shuning uchun biz «qora ishlarni» kompyuterga, aniqrog’i algoritmlarga qo’yib beramiz.

Qisqa path’ni topish uchun barcha pathlarni tekshirib chiqish kerakligi sababli, algoritmlar graph’ni o’qib chiqadi – traversal.

Graph’lar uchun traversal’ning ikki turi bor:

• Depth first search (DFS)
• Breadth first search (BFS)