Graph masalalari qiziq bo’lib, ko’pincha real hayotda uchraydigan muammolarni yechishga yordam beradi. Masalan, otam distribyutor – do’konlarga non yetkazib beruvchi bo’lib ishlaganlarida, shahardagi do’konlarni qanday qilib eng qisqa masofa bosib va/yoki eng qisqa vaqt ichida aylanib chiqish mumkinligi haqida so’ragandilar. Albatta, graph’lar haqida bilmaganim uchun o’shanda ularning masalalariga dasturiy yo’l bilan javob topolmaganman.
Qisqa yo’l topish algoritmi haqida kelgusi mavzularda to’xtalamiz. Ushbu maqolada biz graph’ning bipartite’ligiga tekshiramiz.
Bipartite graph
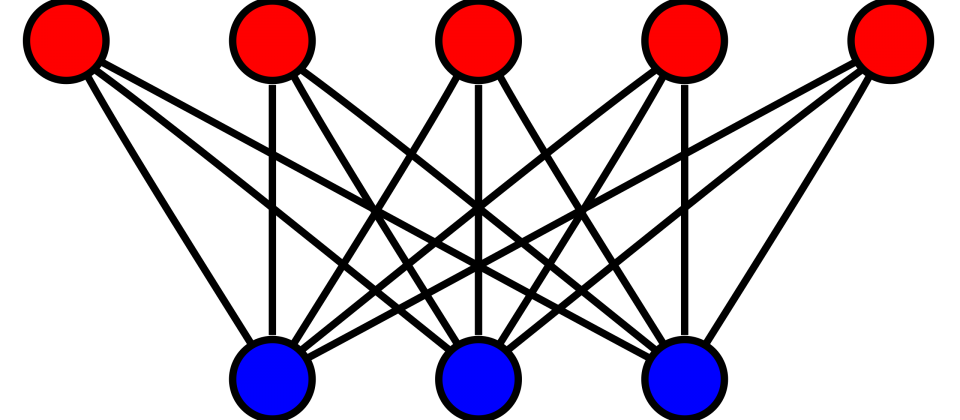
Agar graph’ning har bir vertex’i qarama-qarshi tomondagi vertex’ga bog’lanuvchi ikki subset’ga (qismga) ajraladigan bo’lsa, demak graph – bipartite bo’ladi.
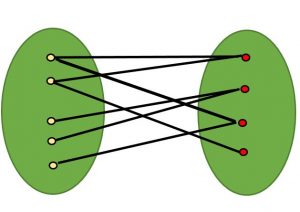
Graph’ning bipartite’ligini aniqlash uchun vertex’larga ikki xil rang, masalan qizil yoki ko’k rang beramiz. Agar barcha qizil rangdagi vertex’lar ko’k rangdagi vertex’larga bog’langan bo’lsa, yoki barcha ko’k rangdagi vertex’lar qizil rangdagi vertex’larga bog’langan bo’lsa, demak graph – bipartite hisoblanadi.
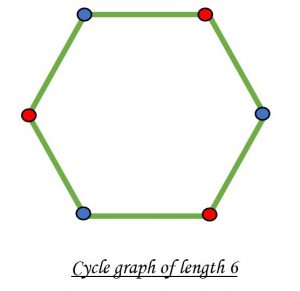
Agar graph aylana shaklda va vertex’lar miqdori juft son bo’lsa, bu graph’ni bipartite deb hisoblash mumkin.
Ishlash tartibi
Graph’ga rang berish uchun depth first search algoritmidan foydalanamiz. Dastlab birinchi vertex’ga qizil rang beramiz. Unga bog’langan vertex’larga ko’k rang, ko’k vertex’larga bog’langan vertex’larga qizil rang va hk berib boramiz. Agar bog’langan vertex’ga allaqachon rang berilgan bo’lsa va uning rangi bog’lovchi vertex’ning rangiga teng bo’lib qolsa – graph bipartite emas. Rang berishda bir-xillik vujudga kelmasa, graph bipartite bo’ladi.
Leetcode’ning 785-masalasi bipartite graph haqida. Uni yechishga harakat qilamiz.
Masalada kirish ma’lumotlari edge list‘da berilgan:
graph = [[1,3],[0,2],[1,3],[0,2]]
Bunda indekslar – vertex, graph[vertex] – edge’lar.