Minimum spanning tree (MST) – undirected graph‘dagi barcha o’zaro bog’langan vertex’larni o’z ichiga olgan (spanning) va aylana bo’lmagan (acyclic) sub-graph’lar ichidan minimum weight‘li sub-graph.
Batafsilroq tushuntiradigan bo’lsak:
- Graph’dagi barcha vertex’lar bog’langan (connected) bo’lsin
- Vertex’lar orasidagi path aylana hosil qilmasin (acyclic).
- Graph’da barcha vertex’larni o’z ichiga olgan bir nechta path bo’lishi mumkin. Bizni qiziqtiradigani – path’lardagi edge weight’larning yig’indisi eng kichkinasi bo’lsin (minimum).
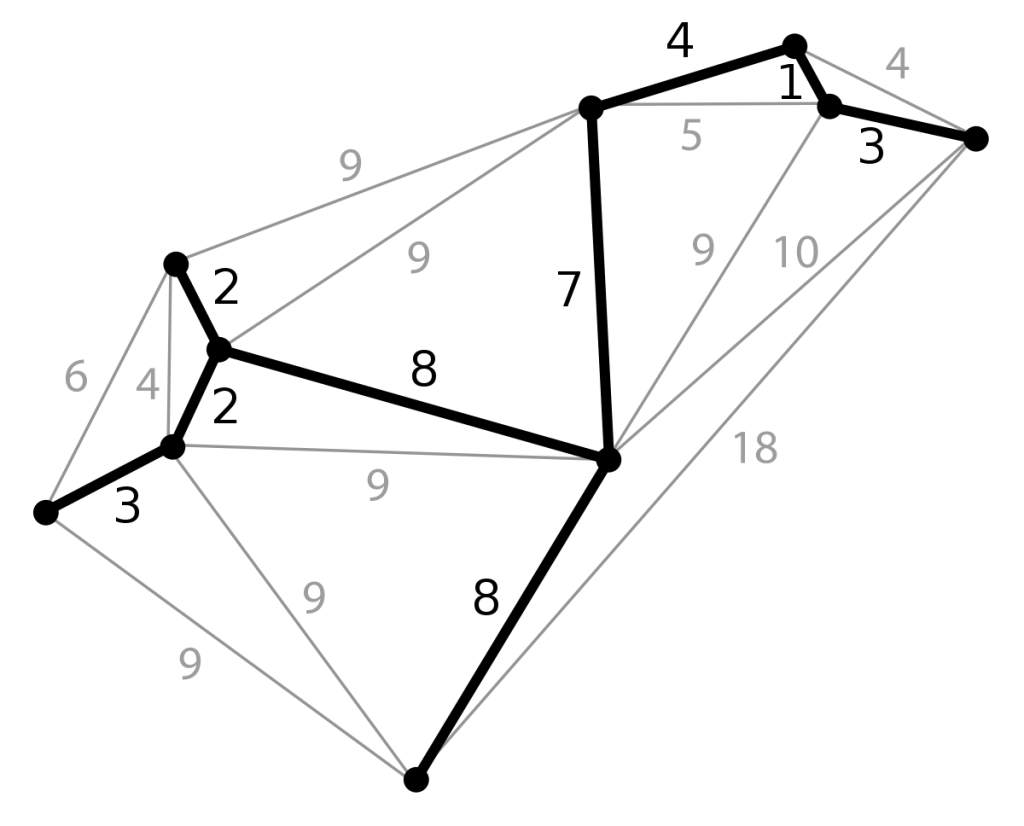
Yuqoridagi graph’dagi MSTning qiymati (cost):
8 + 8 + 3 + 2 + 2 + 3 + 7 + 4 + 1 + 3 = 41
Yuqoridagi graph’da biz boshqa path’ni tanlashimiz mumkin, lekin u holda, boshqa path’dagi weight’lar yig’indisi 41 dan katta bo’lib ketadi. Ya’ni path minimum spanning tree bo’lmay qoladi.
Amaliyotda MSTlardan foydalanish ko’p uchraydi:
- Klasterlarni tahlil qilish
- Real vaqt’da yuzni verifikatsiyasi
- Yaqin yo’lni topish
- Tarmoqni loyihalash (aloqa, elektr, kompyuter, yo’l)
Keyingi mavzularda ko’riladigan masalalar MSTni topish algoritmlari haqida bo’ladi.