Graph processing masalalarini o’rganishni davom ettiramiz.
Minimum cut – graph’ni ikkiga shunday bo’lish kerakki, uning bo’linish edge’lari bir-biriga eng kam (kuchsiz) bog’langan joyi bo’lsin. Oddiyroq aytganda, graph’ni ikkiga bo’lish uchun eng kam harajat / kuch talab etilsin.
Maximum flow – graph’da bir vertex’dan ikkinchi vertex’ga maksimum o’tkazuvchanlik qobilyatini topish masalasi ko’rib chiqiladi.
Minimum cut va maximum flow haqida quyida batafsil to’xtalamiz.
Minimum cut
Bizda pozitiv edge weight’larga ega directed graph mavjud. Boshlang’ich vertext – s, mo’ljal vertex – t. Biz graph’ni minimum kuch sarflagan holda ikkiga bo’lishimiz kerak bo’lsin. Bunda s birinchi qismda, t ikkinchi qismda qoladi.
Kuch / sarf’ni aniqlash uchun edge weight’laridan foydalanamiz, sarfni esa capacity deb ataymiz. Capacity deb, graph ikkiga bo’linganda, ikki qismni bog’lab turuvchi edge’lar weight’larining yig’indisi tushuniladi.
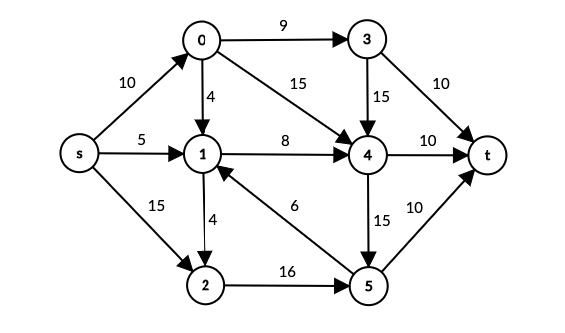
Biz graph’ni ikkiga ajratishga urinib ko’ramiz:
- Agar biz
sni bir tomonda qoldirib, qolgan vertex’larni ikkinchi qismga ajratsak, edge capacity s -> 0, s -> 5, s -> 10 edge weight’larining yig’indisiga teng bo’ladi: 10 + 5 + 15 = 30 - Agar biz s, 1, 2 vertex’larni bir tomonda qoldirib, qolgan vertex’larni ikkinchi qismga ajratsak, edge capacity s -> 0, 1 -> 4, 2 -> 5 edge weight’larining yig’indisiga teng: 10 + 8 + 16 = 34. Capacity hisoblashda ichki bog’lanishlar hisoblanmaydi.
- Agar biz s, 1, 2, 5 vertex’larni bir tomonda qoldirib, qolgan vertex’larni ikkinchi qismga ajratsak, edge capacity s -> 0, 1 -> 4, 5 -> t edge weight’larining yig’indisiga teng: 10+ 8 + 10 = 28
Hisoblashlardan xulosa qiladigan bo’lsak, graph’ni {s, 1, 2, 5} va {0, 3, 4, t} qismlarga ajratish uchun minimum sarf talab qilinar ekan.
Maximum flow
Graph’da bir vertex’dan ikkinchi vertex’ga maksimum o’tkazuvchanlik qobilyatini topish uchun edge’ga yana bir qiymat – flow kiritiladi. Flow – minimum qiymati 0, maksimum qiymati capacity’ga (weight’ga) teng bo’lgan son, bo’lib u edge’ning o’tkazuvchanlik qobilyatini ifodalaydi. Flow’ni quvurlardan qancha suv yuborishni aniqlovchi qiymat deb tasavvur qilsak, minimum = 0, suv o’tmaydi, maksimum = capacity, quvurning o’tkazish qobilyatiga teng.
Shuningdek flow qiymati boshlang’ich va manzil vertex – s va t dan tashqari qolgan har bir vertex’ning muvozanatini, kiruvchi o’tkazuvchanlik (inflow) va chiquvchi o’tkazuvchanligini (outflow) belgilash uchun ham kerak bo’ladi. Bunda muvozanat bo’lishi uchun inflow = outflow bo’lishi kerak.
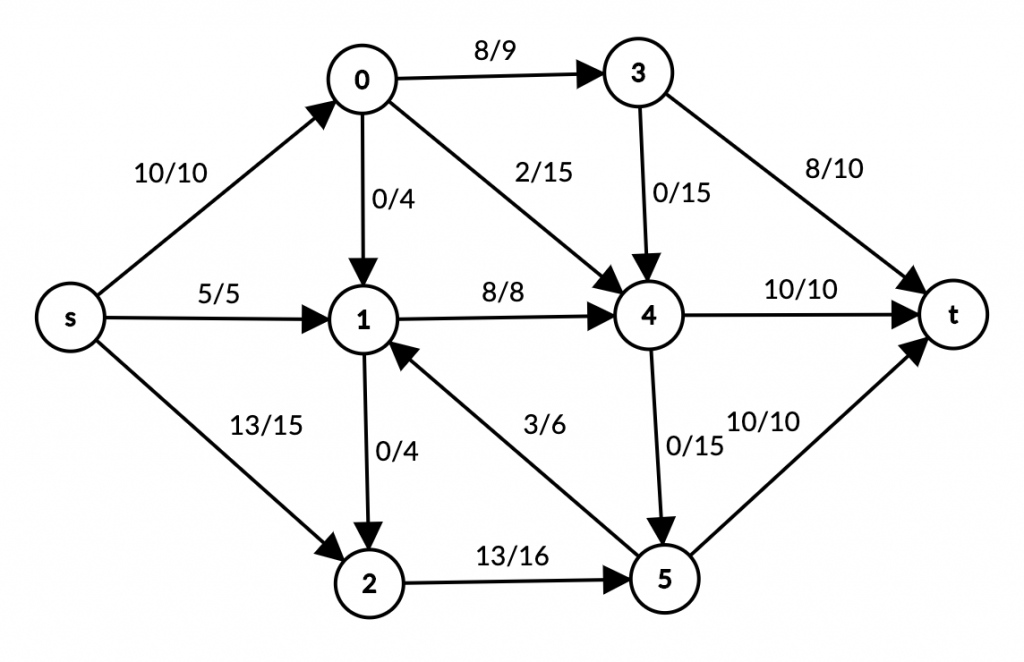
Graph’ga ko’ra, max flow qiymati inflow’ga teng: 8 + 10 + 10 = 28.
Minimum cut ham 28 ga teng edi.
Biz keyingi maqolada maximum flow’ni topish uchun Ford-Fulkerson algoritmini ko’rib chiqamiz.
* * *
Maximum flow va minimum cut ko’rinishidan bir-birining teskarisi bo’lsada, aslida bir biriga teng masalalar. O’zingiz o’ylab ko’ring, graph’ning maksimum o’tkazish qobilyati uning eng kuchsiz bog’langan joyining o’tkazish qobilyatidan katta bo’lolmaydi. Oddiyroq tushuntirganda, quvurlardan suv yuborishda, quvurlarning kichkina ulangan joyining o’tkazish qobilyatidan ko’p suv yubora olmaysiz. Ushbu tenglik maxflow-mincut teoremasi deb ataladi.