Avvalgi maqolada maximum flow allaqachon topilgan graph’ni ko’rib o’tdik. Endi flow’ni qanday hisoblash haqida so’z yuritamiz.
Mana o’sha graph:
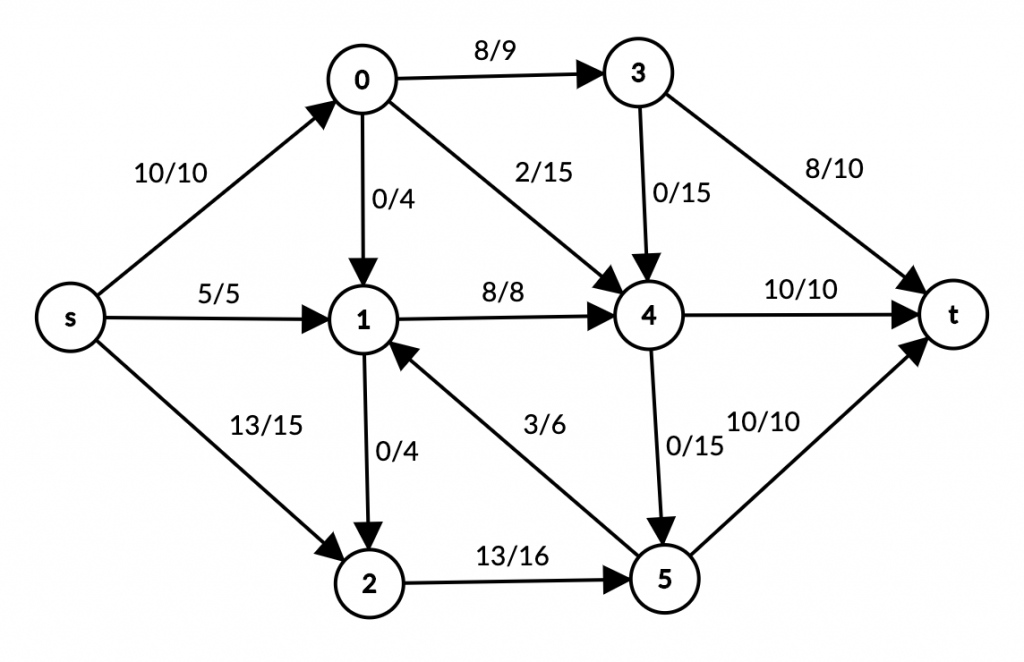
Maximum flow 28 ga teng.
Ammo qanday qilib 28 kelib chiqdi? Qanday qilib flow hisoblandi? Biz hisoblashlarni qadamma-qadam ko’rib o’tamiz.
Ford-Fulkerson algoritmi
Tushunarliroq bo’lishi uchun, graph‘ni yo’nalishga ega quvurlar tarmog’i deb olamiz.
Dastlabki holatida flow hisoblanmagan (quvurlar bo’sh).
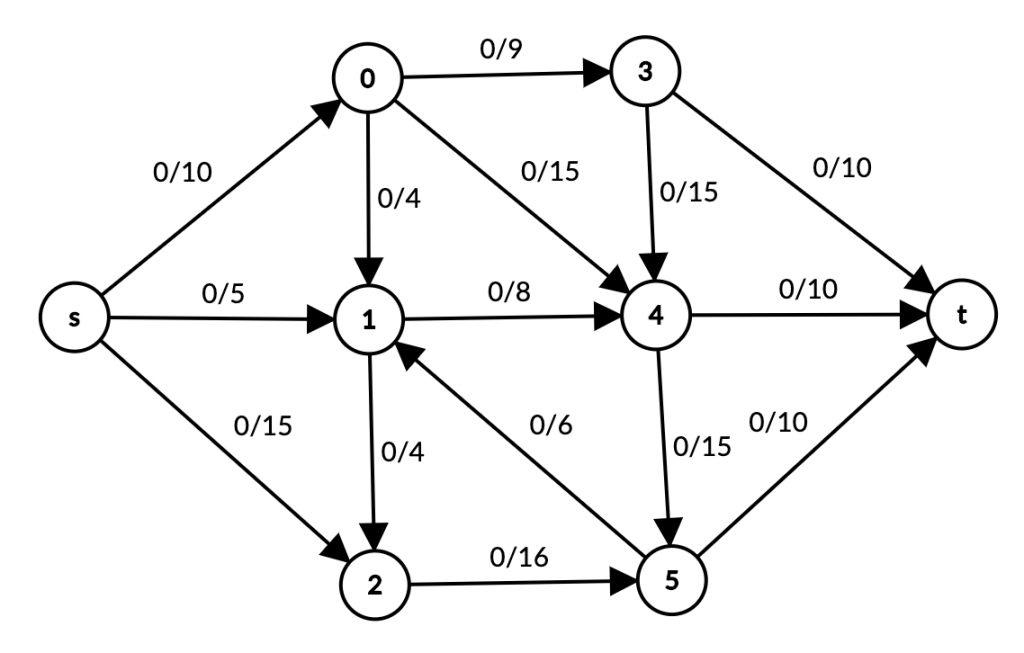
Har bir edge’ning (quvurning) o’tkazish qobilyati – capacity aniq berilgan. Biz bir vaqtning o’zida capacity’dan ko’p flow bera olmaymiz (capacity qiymatidan ko’p suv yubora olmaymiz).
Boshlang’ich nuqta – s dan maximum flow yuborish uning edge capacity’lari yig’indisiga teng – 30. Biz quvurlar tizimining boshlang’ich nuqtasidan maksimum 30 shartli birlik (masalan, litr) suv yuborishimiz mumkin ekan: s -> 0 dan 10, s -> 1 dan 5, s -> 2 dan 15.
Lekin qolgan edge’lar capacity’si boshlang’ich nuqta – s nikidan past, demak biz maksimum 30 yubora olmaymiz. (Quvurlarni yorib yubormaslik uchun) avval s dan t gacha path’dagi edge capacity uchun cheklovlarni hisobga olishimiz kerak.
s dan t ga path’larni (quvurlarni) ko’rib chiqamiz.
s -> 0 -> 3 -> t path’ning bir vaqtda maksimum o’tkazish qobilyati 9 ga teng, sababi 0 -> 3 capacity = 9. Ushbu path’ga max flow beramiz. (quvurlardan suv yuboramiz):
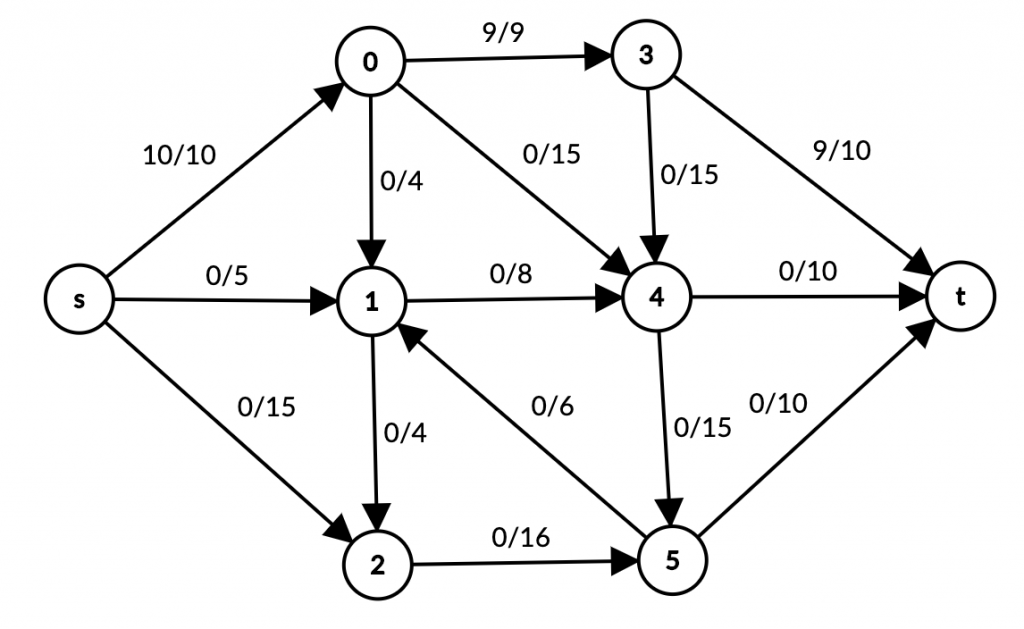
s -> 0 edge’ga yana 1 flow qo’shishimiz (quvurdan yana 1 litr suv yuborishimiz mumkin). 1 qiymati 0 -> 4 -> t dan ketadi.
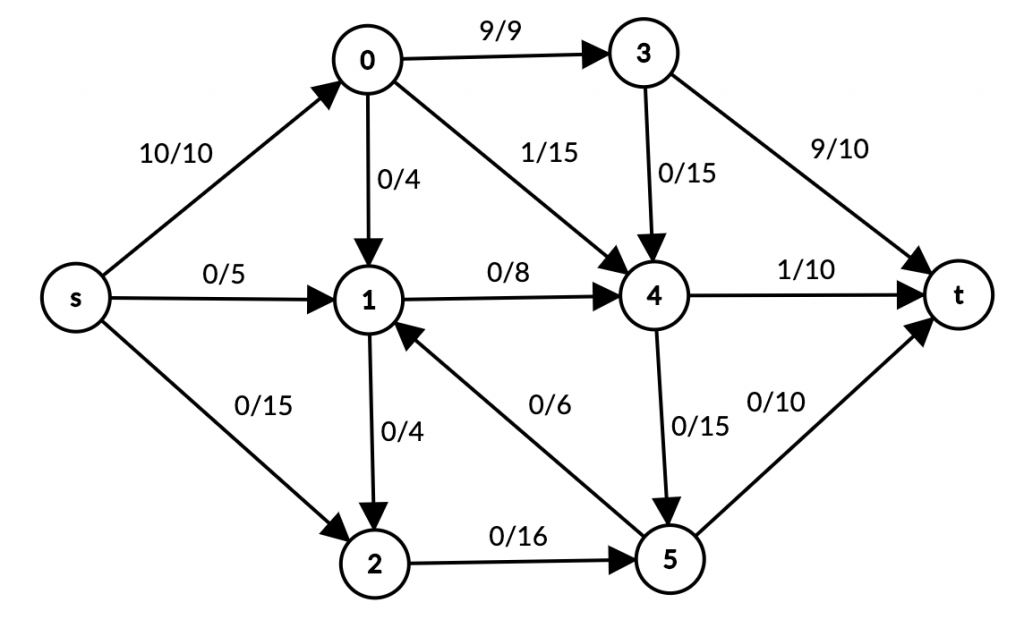
s -> 0 maksimum flow’ga erishdi. s dan keyingi edge’lar orqali t ga path qidiramiz.
s -> 1 -> 4 -> t path topildi. Uning maksimum o’tkazish qobilyati 5, sababi s -> 1 ning capacity’si 5 ga teng. Path edge’lariga 5 qo’shib chiqamiz (quvurlardan 5 litr suv yuboramiz).
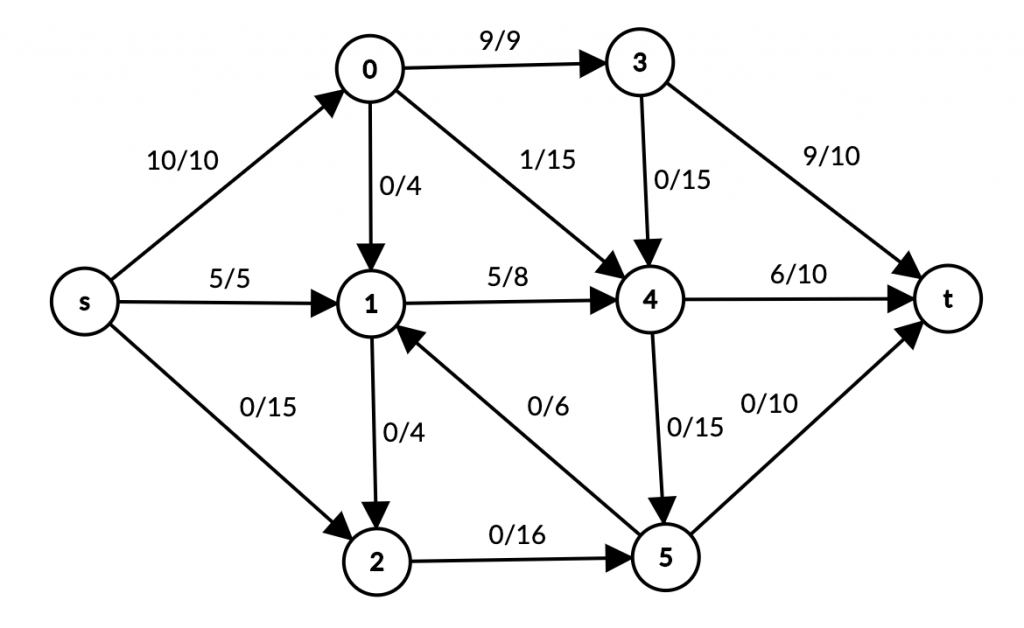
s -> 1 maksimum flow’ga erishdi. Bizda s -> 2 edge bo’sh. s -> 2 orqali t ga path qidiramiz.
s -> 2 -> 5 -> t path topildi. Uning maksimum o’tkazish qobilyati 10 (quvurlardan 10 litr suv yuboramiz):
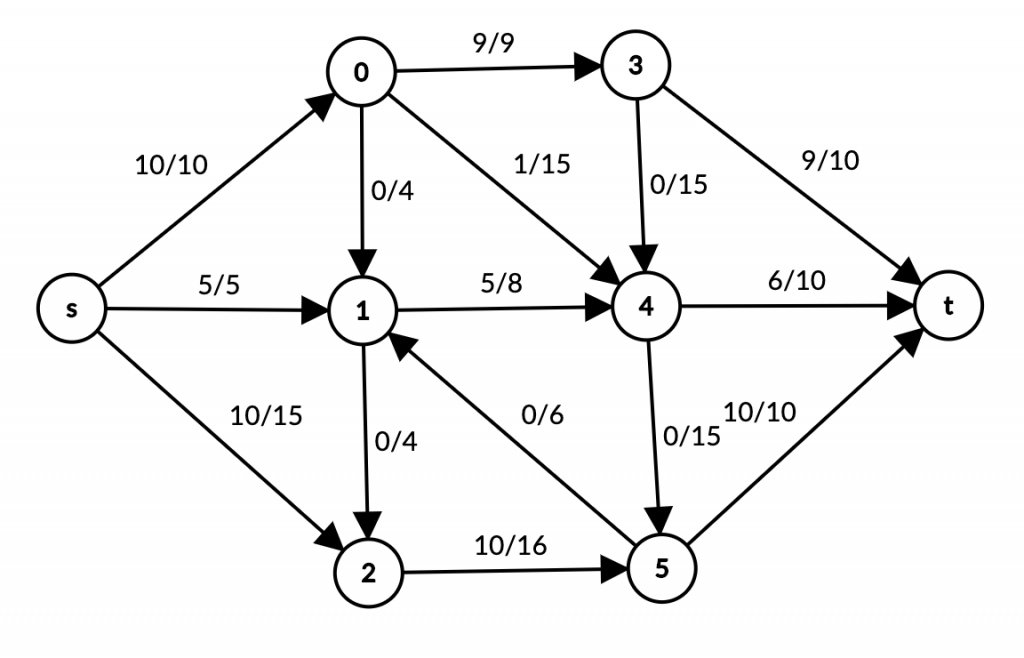
Biz quvurlarning o’tkazish qobilyatidan maksimum darajada foydalanyapmizmi? Hozircha yo’q, s -> 2 edge yana 5 flow qo’shishimiz mumkin. Bizda s dan t gacha yana bo’sh path bormi? Ha, s -> 2 -> 5 -> 1 -> 4 -> t Uning maksimum o’tkazish qobilyati 3, sababi 1 -> 4 da 3 qo’shishga bo’sh joy bor.
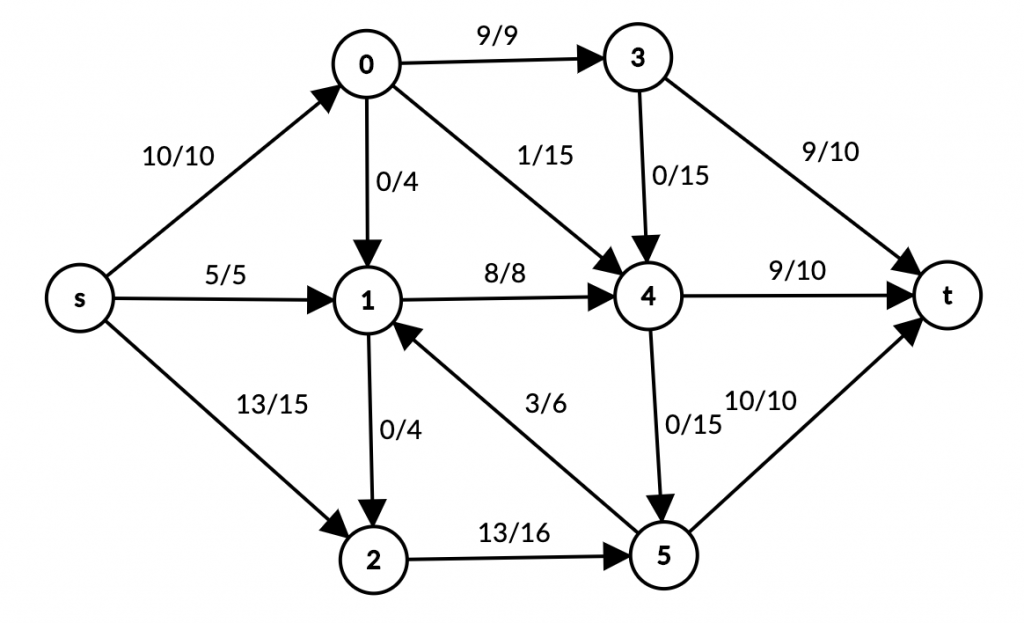
Bizda yana bo’sh path bormi? Yo’q, barcha path’lardagi kamida bitta edge capacity to’lgan: s -> 0, 1 -> 4, 5 -> t. Biz s boshlang’ich nuqtadan t gacha ortiqcha suv yubora olmaymiz.
Graph’ni to’lgan capacity edge’lari bo’yicha ikkiga ajratsak, minimum cut’ni ham topgan bo’lamiz:
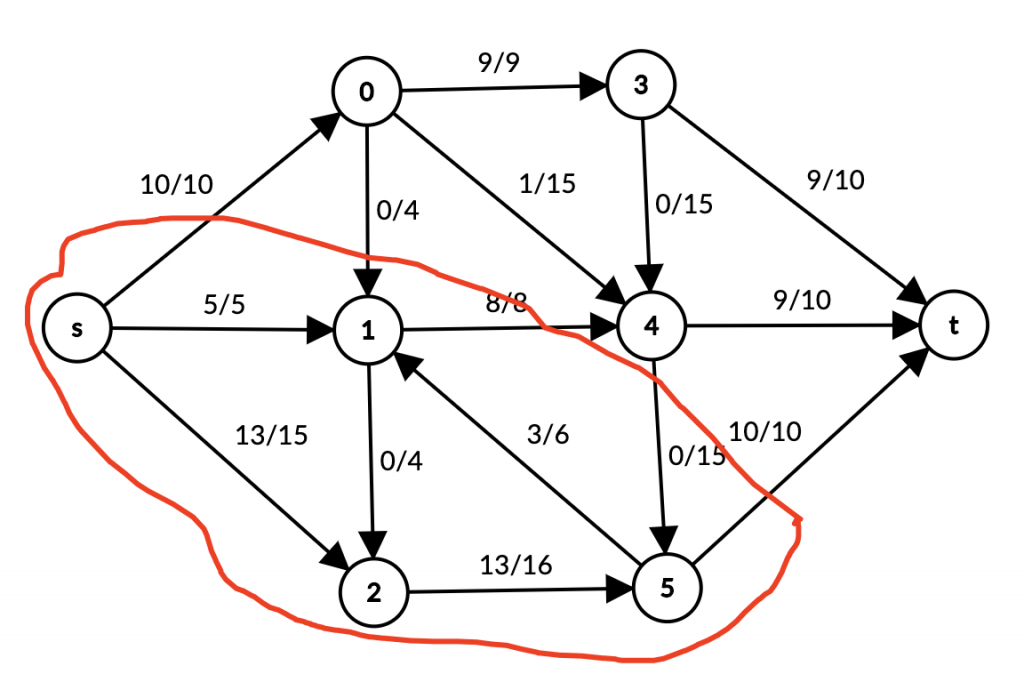
Biz maximum flow’ni topish barobarida, maxflow = mincut teoremasini ham isbotladik.
Natijani sahifaning yuqorisidagi tayyor graph bilan taqqoslaganimizda t ga inflow farq qilyapti, {8, 10, 10} ga {9, 9, 10}. Bu qaysi (s t) path’lariga flow berish tartibiga bog’liq.
Shuningdek, biz reverse flow, flow’ni kamaytirishga ham duch kelmadik. Agar s -> 0 -> 4 -> t path’dan boshlaganimizda, keyinchalik biz 0 -> 4 ni 10/15 dan 2/15 ga kamaytirgan bo’lardik (erinmasangiz, o’zingiz shu yo’l bilan hisoblab ko’ring).