Minimum tahrirlash masofasi deb be’mani tarjima qilinadigan minimum edit distance (yoki ixtirochisi sharafiga Levenshtein distance) algoritmi ikki so’z o’rtasidagi farqlar sonini aniqlashga yordam beradi.
Masalan «kitten» va «sitting» so’zlari orasidagi masofa (farq) 3 chunki bir so’zni ikkinchi so’zga aylantirish uchun 3 ta minimum tahrirlash talab etiladi.
- kitten → sitten (k s ga o’zgaradi)
- sitten → sittin (e i ga o’zgaradi)
- sittin → sitting (ohiriga g qo’shiladi).
Tahrirlash deganda belgi qo’shish, mavjud belgini o’zgartirish yoki belgini o’chirish nazarda tutiladi.
Sovet matematigi Levenshtein tahrirlashlar sonini aniqlash uchun quyidagi formulani taqdim etgan:
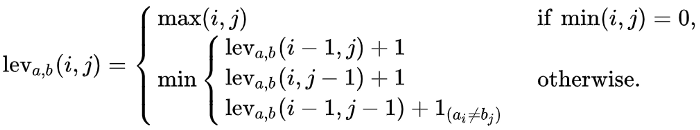
Bu yerda a – birinchi so’z, b – ikkinchi so’z. i – birinchi so’zdagi harfning (belgining) tartib raqami. j – ikkinchi so’zdagi harfning tartib raqami.
Oddiyroq tushuntiradigan bo’lsak, agar i va j ning minimumi 0 ga teng bo’lsa, levenshteyn soni i va j ning maksimumiga teng. Masalan birinchi so’z «hello» bo’lib, ikkinchi so’z «» bo’lsa, u holda i = [1..5], j = 0 ga teng. Shundan kelib chiqib, min(i, j) ham 0 ga teng. Demak levenshteyn soni 5 ga teng bo’ladi.
i = 0, j = 0. min(i, j) = 0. max(i, j) = 0
i = 1, j = 0. min(i, j) = 0. max(i, j) = 1
i = 2, j = 0. min(i, j) = 0. max(i, j) = 2
i = 3, j = 0. min(i, j) = 0. max(i, j) = 3
i = 4, j = 0. min(i, j) = 0. max(i, j) = 4
i = 5, j = 0. min(i, j) = 0. max(i, j) = 5
Formulaning birinchi (oson) shartini ko’rib o’tdik. Agar ikki so’z ham bor bo’lsachi?
Ikki so’zning ham uzunligi 0 dan katta bo’lsa, u holda min(i, j) albatta 0 dan katta bo’ladi. U holda ikkinchi shart ishga tushadi. Ikkinchi shartda shunday deyilgan:
(i – 1, j) uchun levenshteyn sonini topib unga 1ni qo’sh: lev(i-1, j) + 1
(i, j – 1)uchun levenshteyn sonini topib unga 1 ni qo’sh: lev(i, j-1) + 1
(i – 1, j – 1) uchun levenshteyn sonini topib unga agar ai va bj belgilar bir-biriga teng bo’lmasagina 1 ni qo’sh: lev(i-1, j-1) + 1a!=b
Yuqorida topilgan 3 ta sonning orasidan minimumini top. o’sha son levenshteyn soniga teng bo’ladi.
Biz har bir belgini solishtirish uchun, avval o’zidan oldingi belgini solishtirib levenshteyn sonini topgan bo’lishimiz kerak ekan. i yoki j 0 ga teng bo’lganda esa, max(i, j) ni olar ekanmiz. Dynamic programming texnikasiga o’xshayaptimi?
Ha, o’xshayapti, biz formula asosida jadval/matritsani to’ldirib borib, uning pastdan ohirgi yacheykasiga yetganimizda minimum edit distance‘ni topgan bo’lamiz.
Ishlash tartibi
Formulaga qaytamiz. Uning birinchi sharti bo’yicha matritsani to’ldiramiz.
| j → | K | I | T | T | E | N | |
| i ↓ | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| S | 1 | ||||||
| I | 2 | ||||||
| T | 3 | ||||||
| T | 4 | ||||||
| I | 5 | ||||||
| N | 6 | ||||||
| G | 7 |
Keyingi hisoblashlar endi formuladagi ikkinchi shart asosida kechadi.
1.1. (i = 1, j = 1) S va K ni solishtiramiz. U bir-biriga teng emas: levi,j = min([i – 1, j] + 1, [i, j – 1] + 1, [i – 1, j – 1] + 1) = 1
| j → | K | I | T | T | E | N | |
| i ↓ | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| S | 1 | 1 | |||||
| I | 2 | ||||||
| T | 3 | ||||||
| T | 4 | ||||||
| I | 5 | ||||||
| N | 6 | ||||||
| G | 7 |
1.2. S va I ni solishtiramiz. U bir-biriga teng emas: levi,j = min(2 + 1, 1 + 1, 1 + 1) = 2
| j → | K | I | T | T | E | N | |
| i ↓ | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| S | 1 | 1 | 2 | ||||
| I | 2 | ||||||
| T | 3 | ||||||
| T | 4 | ||||||
| I | 5 | ||||||
| N | 6 | ||||||
| G | 7 |
1.3. S va T ni solishtiramiz: levi,j = min(3 + 1, 2 + 1, 2 + 1) = 3
| j → | K | I | T | T | E | N | |
| i ↓ | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| S | 1 | 1 | 2 | 3 | |||
| I | 2 | ||||||
| T | 3 | ||||||
| T | 4 | ||||||
| I | 5 | ||||||
| N | 6 | ||||||
| G | 7 |
1.4. S va T ni solishtiramiz: levi,j = min(4+ 1, 3+ 1, 3+ 1) = 4
| j → | K | I | T | T | E | N | |
| i ↓ | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| S | 1 | 1 | 2 | 3 | 4 | ||
| I | 2 | ||||||
| T | 3 | ||||||
| T | 4 | ||||||
| I | 5 | ||||||
| N | 6 | ||||||
| G | 7 |
1.5. S va E ni solishtiramiz: levi,j = min(5+ 1, 4+ 1, 4+ 1) = 5
| j → | K | I | T | T | E | N | |
| i ↓ | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| S | 1 | 1 | 2 | 3 | 4 | 5 | |
| I | 2 | ||||||
| T | 3 | ||||||
| T | 4 | ||||||
| I | 5 | ||||||
| N | 6 | ||||||
| G | 7 |
1.6. S va N ni solishtiramiz: levi,j = min(6+1, 5+1, 5+1) = 6
| j → | K | I | T | T | E | N | |
| i ↓ | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| S | 1 | 1 | 2 | 3 | 4 | 5 | 6 |
| I | 2 | ||||||
| T | 3 | ||||||
| T | 4 | ||||||
| I | 5 | ||||||
| N | 6 | ||||||
| G | 7 |
2.1. I va K ni solishtiramiz: levi,j = min(1+1, 2+1, 1+1) = 2
| j → | K | I | T | T | E | N | |
| i ↓ | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| S | 1 | 1 | 2 | 3 | 4 | 5 | 6 |
| I | 2 | 2 | |||||
| T | 3 | ||||||
| T | 4 | ||||||
| I | 5 | ||||||
| N | 6 | ||||||
| G | 7 |
2.2. I va I ni solishtiramiz. Harflar bir-biriga teng: levi,j = min([i – 1, j] + 1, [i, j – 1] + 1, [i – 1, j – 1]) = 1
| j → | K | I | T | T | E | N | |
| i ↓ | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| S | 1 | 1 | 2 | 3 | 4 | 5 | 6 |
| I | 2 | 2 | 1 | ||||
| T | 3 | ||||||
| T | 4 | ||||||
| I | 5 | ||||||
| N | 6 | ||||||
| G | 7 |
2.3. I va T ni solishtiramiz: levi,j = min(3+1, 1+1, 2+1) = 2
| j → | K | I | T | T | E | N | |
| i ↓ | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| S | 1 | 1 | 2 | 3 | 4 | 5 | 6 |
| I | 2 | 2 | 1 | 2 | |||
| T | 3 | ||||||
| T | 4 | ||||||
| I | 5 | ||||||
| N | 6 | ||||||
| G | 7 |
2.4. I va T ni solishtiramiz: levi,j = min(4+1, 2+1, 3+1) = 3
| j → | K | I | T | T | E | N | |
| i ↓ | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| S | 1 | 1 | 2 | 3 | 4 | 5 | 6 |
| I | 2 | 2 | 1 | 2 | 3 | ||
| T | 3 | ||||||
| T | 4 | ||||||
| I | 5 | ||||||
| N | 6 | ||||||
| G | 7 |
2.5. I va E ni solishtiramiz: levi,j = min(5+1, 3+1, 4+1) = 4
| j → | K | I | T | T | E | N | |
| i ↓ | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| S | 1 | 1 | 2 | 3 | 4 | 5 | 6 |
| I | 2 | 2 | 1 | 2 | 3 | 4 | |
| T | 3 | ||||||
| T | 4 | ||||||
| I | 5 | ||||||
| N | 6 | ||||||
| G | 7 |
2.6. I va N ni solishtiramiz: levi,j = min(6+1, 4+1, 5+1) = 4
| j → | K | I | T | T | E | N | |
| i ↓ | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| S | 1 | 1 | 2 | 3 | 4 | 5 | 6 |
| I | 2 | 2 | 1 | 2 | 3 | 4 | 5 |
| T | 3 | ||||||
| T | 4 | ||||||
| I | 5 | ||||||
| N | 6 | ||||||
| G | 7 |
Shu tariqa jadvalni to’ldirib boramiz. Hisoblashlar yakunida jadval quyidagi ko’rinishga keladi:
| j → | K | I | T | T | E | N | |
| i ↓ | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| S | 1 | 1 | 2 | 3 | 4 | 5 | 6 |
| I | 2 | 2 | 1 | 2 | 3 | 4 | 5 |
| T | 3 | 3 | 2 | 1 | 2 | 3 | 4 |
| T | 4 | 4 | 3 | 2 | 1 | 2 | 3 |
| I | 5 | 5 | 4 | 3 | 2 | 2 | 3 |
| N | 6 | 6 | 5 | 4 | 3 | 3 | 2 |
| G | 7 | 7 | 6 | 5 | 4 | 4 | 3 |
Ohirgi yacheykadagi son – 3, demak minimum edit distance soni 3 ga teng ekan.
Qaysi harflar tahrirlangan?
Agar aynan qaysi belgilar tahrirlanganini topish kerak bo’lsa, jadvalda ohiridan boshiga qarab tekshirib chiqamiz. Bunda agar ikki harf bir biriga teng bo’lmasa, yacheykadagi sonidan 1 ni ayirib boramiz.
Hozir [i=7, j=6] yacheykada turibmiz. Uning qiymati 3. G va N harflari bir biriga teng emas, demak 3 – 1 = 2. 2 qiymati [i=6, j=6] yacheykadan kelyapti. Agar bir qator yuqoriga ko’tarilsa, harf qo’shilgan bo’ladi. Xulosa – G harfi qo’shilgan.
[6,6] yacheykadamiz. Uning qiymati – 2. N = N, 1 ayirilmaydi. 2 soni [5,5] yacheykadan kelyapti. Agar ikki harf bir-biriga teng bo’lganda, bir qator yuqoriga, bir qator chapga surilsa, harf o’zgarmagan bo’ladi. Xulosa – harf o’zgarmagan.
[5,5] yacheykadamiz. Uning qiymati – 2. I != E. 2 – 1 = 1. 1 soni [4,4] yacheykadan kelyapti. Agar ikki harf bir-biriga teng bo’lmagan holda, bir qator yuqoriga, bir qator chapga surilsa, harf o’zgargan bo’ladi. Xulosa – harf o’zgargan.
[4,4] yacheykadamiz. Uning qiymati – 1. T = T. 1 soni [3,3] yacheykadan kelyapti. Xulosa – harf o’zgarmagan.
[3,3] yacheykadamiz. Uning qiymati – 1. T = T. 1 soni [2,2] yacheykadan kelyapti. Xulosa – harf o’zgarmagan.
[2,2] yacheykadamiz. Uning qiymati – 1. I = I. 1 soni [1,1] yacheykadan kelyapti. Xulosa – harf o’zgarmagan.
[1,1] yacheykadamiz. Uning qiymati – 1. S != K. 1-1 = 0. 0 soni [0,0] yacheykadan kelyapti. Xulosa – harf o’zgargan.
Bizning misolda harf o’chirilishi ro’y bermadi. Agar bir qator chapga surilsa, harf o’chirilgan bo’ladi.