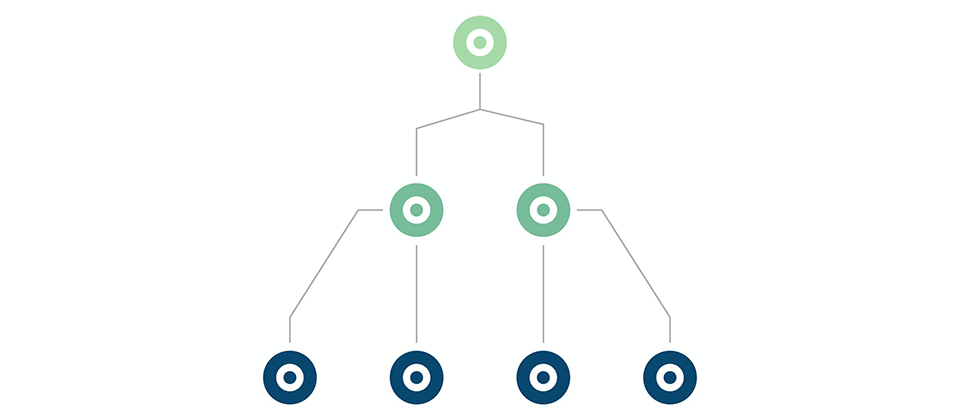
R-way tries
Ushbu mavzu string key’lar qidiruvi uchun mo’ljallangan ma’lumotlar tuzilmasi – tries (trays) haqida bo’ladi. Shu vaqtgacha ko’rib o’tgan ma’lumotlar tuzilmalaridan qidiruv uchun eng yaxshisi red-black tree – key’ni qidirish / qo’shish / o’chirish uchun O(log N) vaqtni kafolatlardi.