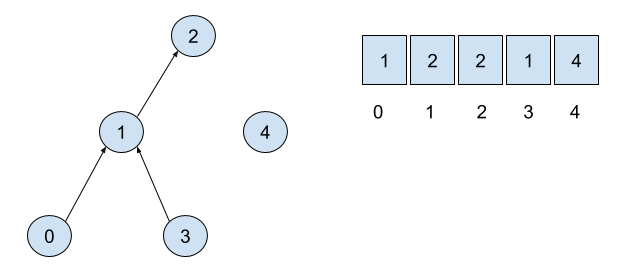
Kompyuter va graph nazariyasida dinamik bog’lanish deb bog’langan komponentlar o’rtasidagi ma’lumotlarni o’zida saqlaydigan ma’lumotlar tuzilmasiga aytiladi. Dinamik bog’lanishga ega sodda ma’lumot tuzilmasiga Disjoint-set (yoki union-find) ni misol qilib keltirish mumkin.
Union-find tushunarli bo’lishi uchun real-hayotdan misol keltiraman. Yomg’ir vaqtida derazadagi suv tomchilarini tasavvur qiling. Ikki tomchi bir biriga yaqin kelganda qaysidir muddatda ular birlashib bitta tomchiga aylanib qoladi. Mana shu birlashish union-find’dagi union qismi.
Dasturlashdagi misol. Bizda juda ko’p node’lar bor va ularning ba’zilari ba’zilari bilan guruhlangan:
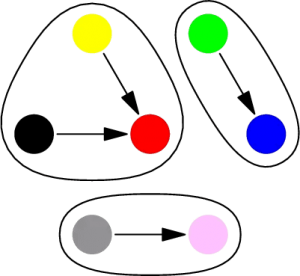
Ikki node’ning bir guruhda ekanligini aniqlash uchun «sariq va qora node’lar bir guruhdami?» deb so’raymiz. Yuqoridagi rasmga ko’ra sariq va qora node ikkisi qizil node’ga bog’langan. Demakki ular orasida bog’lanish bor, ular bir guruhda.
Endi ikki guruh o’rtasida union amalini bajaramiz:

E’tiborga molik jihati, union-find strukturasida ulanishni orqaga qaytarishning, ulangan qismni qayta ajratishning imkoni yo’q.
Bazaviy tushunchaga ega bo’ldik, endi qanday qilib union-find algoritmini amalga oshiramiz?
Bizda quyidagicha node guruhlari bor:

Har bir node o’zida boshqa node’ga ko’rsatkichni (pointer) saqlaydi. Har bir komponentdagi (guruhdagi) bitta node’da pointer bo’lmaydi. Ana o’sha node komponentning o’zagi (root) deb ataladi. Bizning misolda root’lar – qizil, ko’k va pushti node’lar.
Ikki komponentni birlashtirish uchun yana bir pointer qo’shamiz:
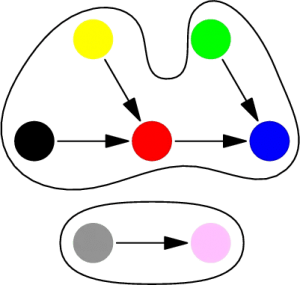
Natijada ko’k node kattalashgan komponentning o’zagi (root), qizil node esa endi root emas.
Yuqorida aytib o’tganimizdek, union-find data structure’ning mazmuni ikki node bir komponent ichida ekanligini aniqlay olishimizda. Buning uchun topish (find) amali – node’larni tekshirib ularning pointeri bo’yicha root’ni qaytarish. Misolimizda biz sariq node’ning root’ini topmoqchi bo’lsak, sariq -> qizil -> ko’k ga kelamiz. Yashilni tekshirib ham biz ko’kga yetib boramiz. Demak sariq va yashil bitta root’da birlashgani uchun ushbu ikki node bitta komponent ichida bo’ladi.
Strukturada node’lar ko’p bo’lganda pointerlar orqali topish qiyin effektiv bo’lmasligi mumkin chunki bunda node’ning root’gacha bo’lgan yo’li uzun bo’lishi mumkin. Union-find qanday yechim beradi? Ikki optimizatsiya:
– Path compression. Biz find amalini bajarganimizda pointerlar orqali topib kelamiz. Aslida union-find uchun yo’lning uzunligi muhim emas. Shuning uchun biz node’ni to’g’ridan to’g’ri root’ga ulab qo’yishimiz ham mumkin. Buni yo’lni qisqartirish (path compression) deyiladi. Qancha ko’p yo’l qisqartirsak, node’ni tekshirish shuncha tezlashadi.
– Merge by rank (Darajasi bo’yicha birlashtirish). Daraxt kabi bir necha darajaga ega ikki komponentni birlashtirganimizda, qisqaroq daraxtni uzunroq daraxtga birlashtirishimiz mumkin. Buning uchun komponentlarning uzunligini saqlashimiz kerak bo’ladi, ammo bu qiyin ish emas.
Dasturlash
Dasturlashda union-find structure uchun array’dan foydalaniladi.
Quyida biz bir necha yo’llarni ko’rib chiqamiz.
Eager approach (Quick-Find)
Data structure: N uzunlikdagi array id[]
Natija: p va q da bir xil id bo’lsa, ular bog’langan bo’ladi.
Find. p va q bir xil id ga ega ekanligini tekshirish
Union. p va q joylashgan komponentlarni birlashtirish uchun id’si id[p] va id[q] ga teng bo’lgan node’larni o’zgartirish.
Yaxshiroq tushunish uchun kodni o’zingiz debug qilib ko’rishingiz mumkin.
Eager approach’ning kamchiligi:
Algoritm quadratic time – O(n^2), chunki n uzunlikdagi array elementlarining barchasini bog’lab chiqish uchun n^2 vaqt ketadi. find() esa constant time. find() constant time bo’lgani kompensatsiyasini union() da to’laymiz. Kvadratik algoritmlar esa katta hajmdagi ma’lumotlar uchun sekin ishlaydi.
Lazy approach (Quick-Union)
Lazy approach’da p va q node’larni bog’lash uchun p’ning root’iga q’ning root’ini beramiz. Tekshirishda esa p va q node’larning root’i bir-biriga tengligini, ya’ni bir root’da ekanligini aniqlaymiz.
Lazy approach ham sekin algoritm, sababi find() da ikki node’ning root’ini topishimiz uchun root’gacha bo’lgan elementlarni tekshirib chiqishimiz kerak. Qo’shimchasiga, union() da bog’lanishlar uzun bo’lib ketishi mumkin.
Weighted quick-union
Yuqoridagi quick-union’ni uzun bog’lamlar hosil bo’lmasligi uchun optimallashtiramiz. Buning uchun har bir bog’lamning uzunligini (bog’lamdagi node’larning sonini) alohida array’da yig’ib boramiz. Ikki bog’lamni qo’shganda esa kichikroq bog’lam root’ini kattaroq bog’lamning root’iga bog’laymiz.
Yana optimallashtirish mumkinmi? Mumkin, uzun bog’lamlardagi node’larni rootga bog’lash orqali. Buni path compression deyiladi.
Kodlarni Githubda ham ko’rib chiqishingiz mumkin: https://github.com/Webmaxor/leetcode-solutions/tree/master/algorithms/union-find
Savollarni githubda yangi tema (New issue) ochib yozib qoldiring: https://github.com/Webmaxor/leetcode-solutions/issues
Xulosa
Uzun maqolada Union-Find’ni aniq, tushunarli yozdim deb o’ylamayman. Menimcha kodni ishlatib, debug qilib ko’rganda, algoritm ishlashini ko’proq tushunish mumkin bo’ladi.
* * *
Mavzu bo’yicha savollarni Github’dagi Webmaxor / leetcode-solutions repository’da yozishingiz yoki kodda Reference in new issue ni bosib, qoldirishingiz mumkin.