Quicksort bilan tanishib chiqqan bo’lsangiz, algoritmda bo’luvchi element (pivot) array’ni ikkiga bo’ladi. Bunda array[pivot]’ning chap tarafida undan kichkina qiymatlar, o’ng tarafida undan katta qiymatlar o’rin oladi. Ushbu algoritmning kamchiligi shundaki – ro’yhatda bir xil qiymatlar ko’p uchraydigan bo’lsa, ishlash vaqti orta boshlaydi. Bir xil qiymatli elementlardan iborat array’ni tartiblashda esa, Quicksort’ning time complexity‘si ~ O(1/2 N2) bo’lib ketadi.
Algoritmni optimallashtirish uchun array[pivot]’ga teng elementlarni tekshirishni to’xtatish tavsiya qilinadi, shunda time complexity ~ O(N lg N) gacha kamayadi. Mana shu optimallashtirish uch tomonlama bo’lish (3-way partitioning) deb ataladi. 3-way partitioning algoritmining yana bir nomi – Dutch National Flag.
3-way partitioning’da maqsad, array’ni uchga shunday bo’lish kerakki:
- v (v = array[pivot]) ga teng elementlar arrayning o’rtasida yig’ilsin
- v chegarasining (lt) chap tarafida v dan kichkina sonlar joylashsin
- v chegarasining (gt) o’ng tarafida v dan katta sonlar joylashsin
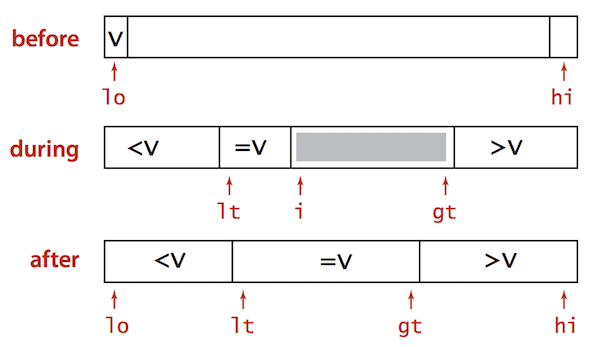
3-way partitioning algoritmi ishlash tartibi
Bizda tartiblanmagan array bor:
[6, 9, 4, 2, 8, 5, 2, 6, 5, 7, 2, 7, 6]
Boshlang’ich ma’lumotlar:
- v sifatida Quicksort’dagidek arrayning birinchi elementi qiymatini olamiz. v = 6.
- arrayni boshidan ohirigacha tekshirishni boshlaymiz. Sikl boshida i = 0.
- v’ning chap chegarasi – lt = 0. array[lt] = 6, o’ng chegarasi – gt = array.length – 1. array[gt] = 6
Ishlash tartibi:
- Siklni ishga tushiramiz, sikl sharti i > gt bo’lgunga qadar davom ettiramiz.
- (array[i] <v): array[lt] va array[i] o’rnini almashtiramiz; lt va i ni bittaga oshiramiz (increment).
- (array[i] > v): array[gt] va array[i] o’rnini almashtiramiz; gt ni bittaga kamaytiramiz (decrement).
- (array[i] == v): i ni bittaga oshiramiz (increment).
- i > gt bo’lganda siklni to’xtatamiz.
- array’ning v chap chegarasidan (lt) chap qismi hamda o’ng chegarasidan (lt) o’ng qismi uchun tartiblashni qaytadan boshlaymiz (rekursiya).
1-sikl. i = 0, lt = 0, gt = 12.
array[i] = 6 == v, i++ . Array’da o’zgarish bo’lmaydi:
[6, 9, 4, 2, 8, 5, 2, 6, 5, 7, 2, 7, 6]
2-sikl. i = 1, lt = 0, gt = 12.
array[i] = 9 > v, array[gt] va array[i] o’rnini almashtiramiz. gt–.
[6, 6, 4, 2, 8, 5, 2, 6, 5, 7, 2, 7, 9]
3-sikl. i = 1, lt = 0, gt = 11.
array[i] = 6 == v, i++. Array’da o’zgarish bo’lmaydi.
[6, 6, 4, 2, 8, 5, 2, 6, 5, 7, 2, 7, 9]
4-sikl. i = 2, lt = 0, gt = 11.
array[i] = 4 < v. array[lt] va array[i] o’rni almashadi. lt++, i++.
[4, 6, 6, 2, 8, 5, 2, 6, 5, 7, 2, 7, 9]
5-sikl. i = 3, lt = 1, gt = 11.
array[i] = 2 < v, array[lt] va array[i] o’rni almashadi. lt++, i++.
[4, 2, 6, 6, 8, 5, 2, 6, 5, 7, 2, 7, 9]
6-sikl. i = 4, lt = 2, gt = 11.
array[i] = 8 > v, array[gt] va array[i] o’rni almashadi. gt–.
[4, 2, 6, 6, 7, 5, 2, 6, 5, 7, 2, 8, 9]
7-sikl. i = 4, lt = 2, gt = 10.
array[i] = 7 > v, array[gt] va array[i] o’rni almashadi. gt–.
[4, 2, 6, 6, 2, 5, 2, 6, 5, 7, 7, 8, 9]
8-sikl. i = 4, lt = 2, gt = 9.
array[i] = 2 < v. array[lt] va array[i] o’rni almashadi. lt++, i++.
[4, 2, 2, 6, 6, 5, 2, 6, 5, 7, 7, 8, 9]
9-sikl. i = 5, lt = 3, gt = 9.
array[i] = 5 < v. array[lt] va array[i] o’rni almashadi. lt++, i++.
[4, 2, 2, 5, 6, 6, 2, 6, 5, 7, 7, 8, 9]
10-sikl. i = 6, lt = 4, gt = 9.
array[i] = 2 < v. array[lt] va array[i] o’rni almashadi. lt++, i++.
[4, 2, 2, 5, 2, 6, 6, 6, 5, 7, 7, 8, 9]
11-sikl. i = 7, lt = 5, gt = 9.
array[i] = 6 == v. i++. Arrayda o’zgarish bo’lmaydi.
[4, 2, 2, 5, 2, 6, 6, 6, 5, 7, 7, 8, 9]
12-sikl. i = 8, lt = 5, gt = 9.
array[i] = 5 < v. array[lt] va array[i] o’rni almashadi. lt++, i++.
[4, 2, 2, 5, 2, 5, 6, 6, 6, 7, 7, 8, 9]
12-sikl. i = 9, lt = 6, gt = 9.
array[i] = 7 > v. array[gt] va array[i] o’rni almashadi. Aniqrog’i o’zgarish bo’lmaydi, chunki i = gt. gt–.
[4, 2, 2, 5, 2, 5, 6, 6, 6, 7, 7, 8, 9]
i = 9, gt = 8 bo’lib qolgani uchun, sikl to’xtatiladi. Endi array’ning v chap chegarasidan (lt) chap qismi hamda o’ng chegarasidan (lt) o’ng qismi uchun tartiblashni qaytadan boshlaymiz (rekursiya).
[4, 2, 2, 5, 2, 5, ...]
[..., 7, 7, 8, 9]
Ishlash prinsipini tushuntira oldim deb umid qilaman.
Kod
Note: Funksiya faqat integer sonlarni to’g’ri tartiblaydi. Harflarni yoki string sonlarni to’g’ri tartiblash uchun «>» dan boshqa amalni ishlatish kerak. Masalan, ES6 uchun String.prototype.localeCompare() ni ishlatib ko’ring.
Kod Githubda: https://github.com/Webmaxor/leetcode-solutions/blob/master/algorithms/sorts/quicksort-3-way.js
Qo’shimcha optimallashtirish
Yuqoridagi misolda e’tibor bergan bo’lsangiz, 6-siklda 7 sonining o’rni ikki marta almashdi. aslida 7 sonini biz v dan katta bo’lgani uchun joyida qoldirsak bo’lardi. Muammo bu yerda batafsilroq tushuntirilgan:
Daykstra’ning biz ko’rib o’tgan algoritmining ishlash tartibi shunday. Biz kodni sodda, tushunarli qoldirish hisobiga ortiqcha almashtirishlarga ko’z yumganmiz. Ortiqcha almashtirishlardan qochish mumkinmi? Mumkin, boshqacharoq algoritm yozish bilan.
* * *
Mavzu bo’yicha savollarni Github’dagi Webmaxor / leetcode-solutions repository’da yozishingiz yoki kodda Reference in new issue ni bosib, qoldirishingiz mumkin.