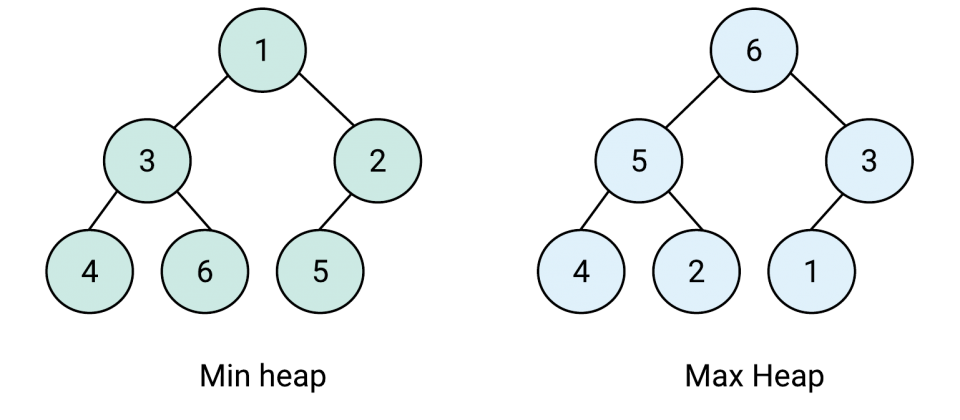
Binary Heap ma’lumotlar to’plami

Binary heap – har bir tuguni (node) maxsus tartiblangan va complete binary tree.

Complete binary tree nima ekanligi haqida bu yerda tushuntirib o’tilgani uchun, maxsus tartiblangan ma’nosiga to’xtalamiz.

Binary heap bo’lishi uchun tree’da ma’lumotlar shajara bo’yicha o’sish tartibida (max heap) yoki kamayish tartibida (min heap) joylashgan bo’lishi kerak.

1. Max-Heap bo’lishi uchun har bir node’ning qiymati uning parent node’ining qiymatidan kichik yoki teng bo’lishi kerak. Eng katta qiymat root’da bo’ladi. Qoida tree’dagi barcha node’lar uchun amal qiladi.
2. Min-Heap bo’lishi uchun har bir node’ning qiymati uning parent node’ining qiymatidan katta yoki teng bo’lishi kerak. Eng kichkina qiymat root’da bo’ladi. Qoida tree’dagi barcha node’lar uchun amal qiladi.

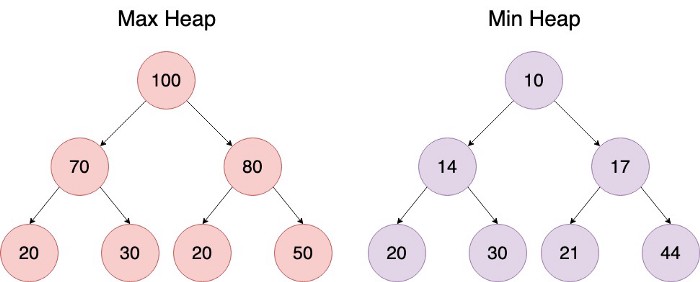
Binary heap nima uchun kerak?

Qisqa javob – heap’dagi eng katta (yoki eng kichik) elementni topish uchun kerak. Bunda binary heap tuzilishi tree bo’lgani uchun eng pastki elementdan eng yuqori elementga chiqish uchun O (log N) urinish lozim. Masalan yuqoridagi rasmda har bir tree’da 7 ta node bo’lsa, pastdan yuqoriga chiqish – log₂7 = 2.8 ~ 2 ta urinishda bo’ladi.

Priority queue maqolasida biz ro’yhatdan eng katta va eng kichik elementni topishni ko’rgan edik. Uning kamchiligi – tartiblanmagan array uchun eng katta (yoki eng kichik) elementni topishda time complexity O(N) bo’lib ketayotgan edi. Tartiblangan array uchun esa, eng katta (eng kichik) elementni topish O(1) bo’ladi, lekin bunda array element qo’shganimizda har safar array’ni tartiblashga majbur bo’linardi – O(N log N).

Demak, Binary heap Priority queue’dan ko’ra samaraliroq ishlaydi. Qo’shish va o’chirish – binary tree’dagi kabi O (log N).

Binary heap’ning kamchiligi – u faqat eng katta (eng kichkina) elementlarni tezda topish imkonini beradi. Boshqa qiymatdagi elementlarni topish uchun heapni «titkilab» chiqish kerak. Sababi binary heap – tartiblanmagan. Tabiiyki tartiblanmagan ro’yhatdan qidirish O(N) vaqtni oladi. Masalan yuqoridagi rasm’dan 30 sonini topish uchun heap’ning hamma elementlari tekshirib chiqish kerak bo’ladi.

Kodda ifodalash

Binary heap uchun double pointer’li linked list ishlatish shartmas. Shunchaki array bilan ham ifodalasa bo’ladi.

Amallar osonroq bo’lishi uchun array[0] ni bo’sh qoldiramiz, keyin heap qiymatlarini kiritamiz. Bizda Max heap’ni kodda ifodalash

const array = [null, 100, 70, 80, 20, 30, 20, 50]

Min heap:

const array = [null, 10, 14, 17, 20, 30, 21, 44]

Agar biz array’dan i-nchi elementni ko’rsak:

• uning parent’i – floor (i-1)/2 indeksda;
• uning chap child’i – 2 * i indeksda;
• uning o’ng child’i – 2 *i + 1 indeksda.

Binary heap ustida amallar

Priority queue’da bo’lgani singari, Binary heap ustida ham ikkita amal bor. Qo’shish (insert yoki enqueue) va eng katta (eng kichik) qiymatini o’chirish (delete yoki dequeue). Shuningdek qo’shilgan va o’chirilgan elementlardan so’ng, heap’ning tartibini to’g’rilash uchun ichki – cho’ktirish (sink) va ko’tarish (swim) amallari ham mavjud.

Insert. Heap’ga node (element) qo’shish uchun:

1. Elementni tree’ning eng pastiga qo’shamiz (array’ning ohiriga qo’shamiz).
2. Qo’shilgan elementning parent’iga qaraymiz. Agar parent’i o’zidan katta bo’lsa, ularning o’rnini almashtiramiz.
3. Solishtirish va almashtirishlarni element parent’idan katta bo’lguncha davom ettiramiz.

Delete. O’chirish’da biz eng katta (yoki eng kichik) qiymati root’da joylashganini bilganimiz uchun ishimiz osonroq, o’chiriladigan elementni topish O(1) vaqt oladi.

O’chirish uchun:

1. root elementni ohirgi element bilan o’rnini almashtiramiz: array[1] ni array[array.length – 1] bilan. Keyin ohirgi elementni o’chiramiz.
2. yangi root’ni uning child’lari bilan solishtiramiz. Agar u child’dan kichik bo’lsa (min heap uchun – child’dan katta bo’lsa), ularning o’rnini almashtiramiz. Ikki child’dan ham kichkina bo’lib qolganda kattaroq qiymatdagi child bilan o’rnini almashtiramiz.
3. shu tariqa solishtirish va almashtirish bilan elementni uning child’larida katta holda qolgunga qadar davom ettiramiz.

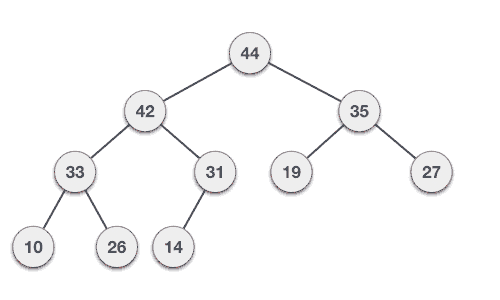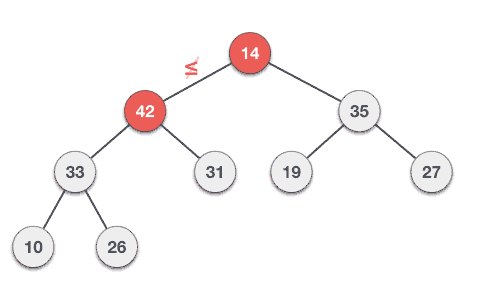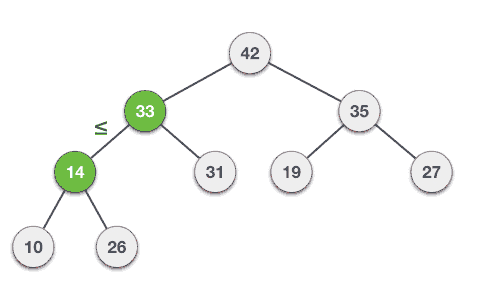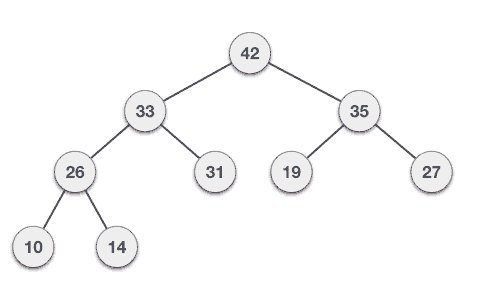
Qo’shish va o’chirish amallarini qanday ishlashini bilib olgach, istalgan tartiblanmagan array’dan binary heap hosil qilishimiz mumkin.

Kod

Priority queue kabi, Binary heap’da amallar bittadan ko’p bo’lgani uchun API yozamiz.

Kod Githubda: https://github.com/Webmaxor/leetcode-solutions/blob/master/algorithms/priority-queues/binary-heap.js

* * *

Mavzu bo’yicha savollarni Github’dagi Webmaxor / leetcode-solutions repository’da yozishingiz yoki kodda Reference in new issue ni bosib, qoldirishingiz mumkin.