Binary search tree bilan tanishib chiqqan bo’lsangiz, ular uchun barcha amallar – search / insert / delete’da worst case – O(N) ga, ya’ni daraxtning uzunligiga teng edi (aniqrog’i, binary search tree – degenerate bo’lganda).
Balanced search tree‘da biz binary search tree’ning uzunligini kamaytirish hisobiga, worst case’ni O (log N) gacha tushiramiz.
Balansni kafolatlash uchun, dastlabki qadam – binary search tree node’larida bittadan ko’p qiymat berish hisoblanadi. Bu 2-3 search tree‘ni ishlatgan holda amalga oshiriladi.
2-3 search tree
2-3 search tree – samaradorlikni oshirishga qaratilgan balanced search tree’ning bir ko’rinishi. U node’larga 1 yoki 2 ta qiymat berishni va node child’larida 3 ta node yoki 2 ta node bo’lishini nazarda tutadi.
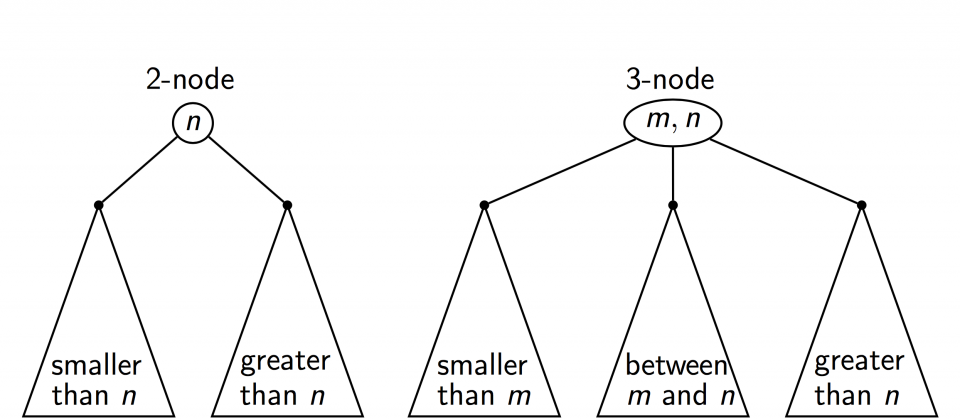
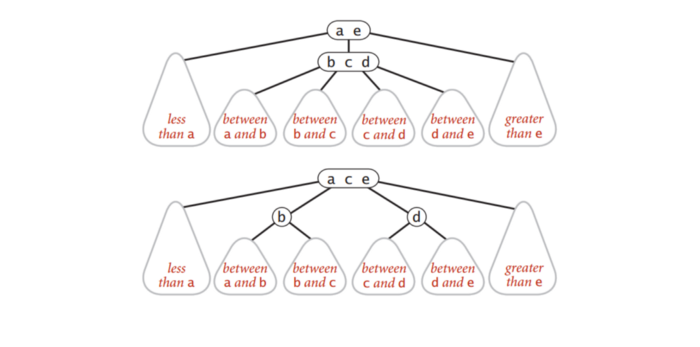
2-node. bitta qiymat, ikkita child. Chap child parent’dan kichik va o’ng child parent’dan katta (binary search tree’dagidek).
3-node. ikkita qiymat, uchta child. Chap child – parent’dagi ikki qiymatdan ham kichik; o’rtadagi child – ikki qiymat oralig’ida (kichik qiymatdan katta va katta qiymatdan kichik); o’ng child – parent’dagi ikki qiymatdan ham katta.
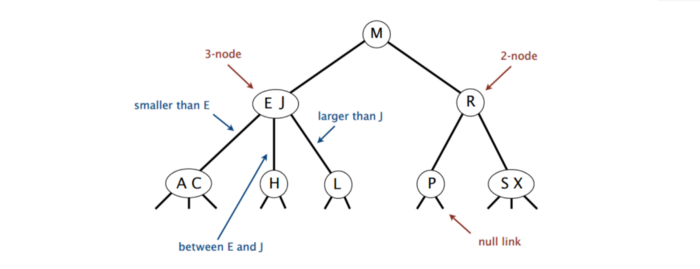
2-3 tree hususiyatlari
- Mukammal balansga ega: root’dan leaf’gacha bo’lgan har bir yo’l bir xil uzunlikka ega.
- Symmetrik tartibda: Har bir node o’zining chap child’idagi barcha node’lardan katta, o’zining o’ng child’idagi barcha node’lardan kichik. 3-node holatida esa, o’rtadagi child node’lari node’ning ikki qiymati oralig’ida.
2-3 tree’da amallar
Biz 2-3 tree uchun kod yozmaymiz, chunki 2-3 tree ishini ifodalash – ayniqsa qo’shish (insert) va o’chirish (delete) uchun qiyin, juda ko’p shartlarni hisobga olish kerak bo’ladi. Shu sababli faqat nazariyasini ko’rib chiqamiz.
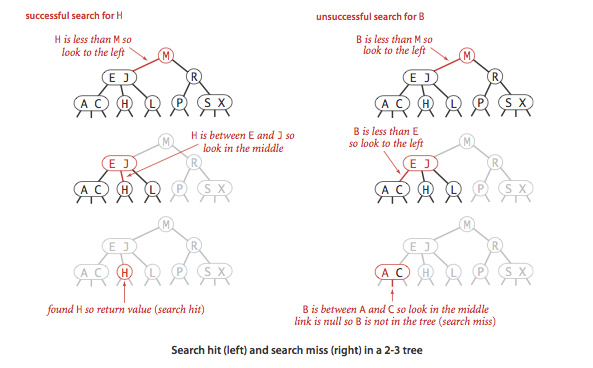
Search. Qidiruv huddi binary search tree‘dagidek bo’ladi. Yagona farqi – uch child’li node’da qidiruv o’rtadagi child’dan davom etishi mumkin.
- Agar qidirilayotgan element node’ning qiymat(lar)idan kichik bo’lsa, qidiruv chap child’dan davom ettiriladi.
- Agar qidirilayotgan element node’ning qiymat(lar)idan katta bo’lsa, qidiruv o’ng child’dan davom ettiriladi.
- Agar qidirilayotgan element 3 child’li node’ning ikki qiymati orasida bo’lsa, o’rtadagi child’dan davom ettiriladi.
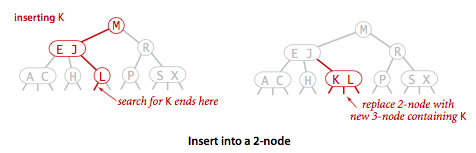
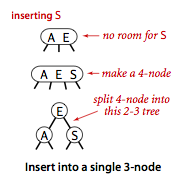
Insert (2-node). Dastlab qo’shilayotgan element qidiriladi. Agar qidiruv 2-node’da to’xtasa, shunchaki element ikkinchi key sifatida qo’shiladi va node 3-node’ga aylanadi. Binary search tree’da biz yangi child qilib qo’shgan bo’lardik, to’g’rimi? 2-3 tree’da ikkinchi key bo’lib qo’shiladi. Sababi? Tree’ni mukammal balansda ushlab turish uchun.
Insert (3-node). Qidiruv 3-node’da to’xtadi. Bunday holatda yangi key uchun joy node’da yo’q. Qo’shishni amalga oshirish uchun 3-node’ni 4-node’ga o’zgartiramiz (3 qiymatli node). Oddiy aytganda, node’ga 3-qiymatni qo’shamiz.
Keyin 4-node’ni 3 ta 2-node’ga o’zgartiramiz.
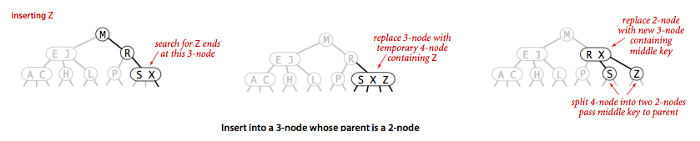
Insert (parent node’i 2-node bo’lgan 3-node). Qidiruv parenti 2-node bo’lgan 3-node’da to’xtadi. Bunday holatda ham vaqtincha 4-node’ga aylantiramiz, lekin o’rta key uchun yangi node qo’shmasdan, o’rta key’ni 2-node parent’ga qo’shamiz (Rasmda tushunarliroq).
Insert (parent node’i 3-node bo’lgan 3-node). Bunda ham vaqtincha 4-node’ga aylantiramiz, keyin o’rtadagi key’ni parent’ga qo’shamiz. Parent 3-node bo’lgani uchun, yangi key qo’shilgach 4-node bo’lib qoladi. Parent uchun ham transformatsiyani – o’rtadagi key’ni parentga berish amaliyotini qo’llaymiz. Shu tariqa, 2-node’li parent’ga yetmagunimizcha yoki root’da 3-node qilmagunimizcha, 4-node’larning o’rta key’ini parentga berib boramiz.

2-3 tree’da transformatsiya
Transformatsiya deb 4-node’ni bo’lishga aytiladi.
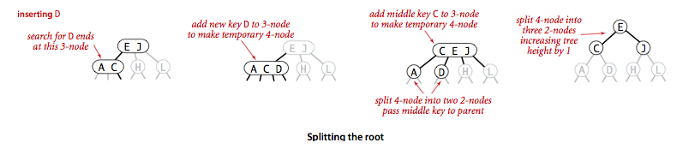
2-3 tree’da tree’ uzunligi faqat root 4-node bo’lib qolgandagina bittaga oshiriladi. Bunda 4-node 3 ta 2-node’ga ajratiladi. O’rta qiymatdagi 2-node parent bo’lsa, kichigi left child, kattasi right child bo’ladi. Faqat root’dan uzunlikni oshirish bizga 2-3 tree’ning mukammal balansda qolishini ta’minlaydi.
Tahlil
Tree’da barcha operatsiyalar uchun worst case tree’ning uzunligiga teng. 2-3 tree’da biz mukammal balansli tree’ga erishganimiz uchun barcha operatsiyalar uchun worst case O(log N) ga tushadi.
- worst case – tree’da barcha node’lar 2-node. Tree uzunligi log N ga teng
- best case – tree’da barcha node’lar 3-node. Tree uzunligi log3 N