AVL-tree (kashfiyotchilari Adelson-Velsky va Landis’lardan olingan) yana bir balanslangan binary search tree. AVL-tree’ga o’tishdan oldin, balanced binary tree haqida eslab olamiz.
Balanced binary tree. Agar binary tree’ning uzunligi (height) O(log n) bo’lsa, balanced binary tree deyiladi. Bunda n – tree’dagi node’lar soni.
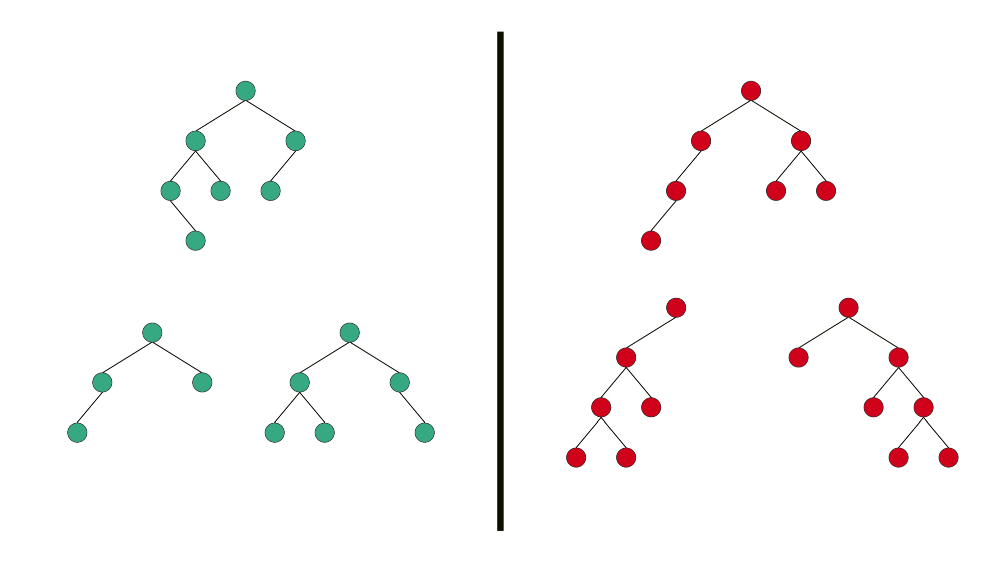
Image credit: https://towardsdatascience.com/5-types-of-binary-tree-with-cool-illustrations-9b335c430254
Demak, balans bo’lishi uchun o’ng va chap child’larning uzunligi bir xil bo’lishi yoki uzunlik −1 ≤ x ≤ 1 orasida farqlanishi kerak.
Red-black tree esingizdami? U daraxtni balansda ushlab turish uchun node’larni chapga yoki o’ngga burish yoki ranglarni almashtirish amallarini bajarardi.
Biz o’rganmoqchi bo’lgan AVL-tree – balans bo’lishi uchun node’larni chapga yoki o’ngga burish amallarini bajaradi. Ya’ni AVL-tree aslida qizil bog’lanishlari yo’q bo’lgan Red-black tree ekan. Tarix aslida bu tarifning xato ekanligini aytadi, sababi AVL-tree tushunchasi 1966-yilda, 2-3 tree paydo bo’lmasidan avval o’ylab topilgan.
AVL-tree ga qo’shish (Insert)
Qo’shish odatiy uslubda, Binary Search tree’dagi kabi bo’ladi. Element qo’shib bo’lingach, tree’ning balansi tekshiriladi. Lozim bo’lganda, balans to’g’rilanadi.
Quyidagi AVL-tree ga element qo’shishni ko’rib chiqamiz.
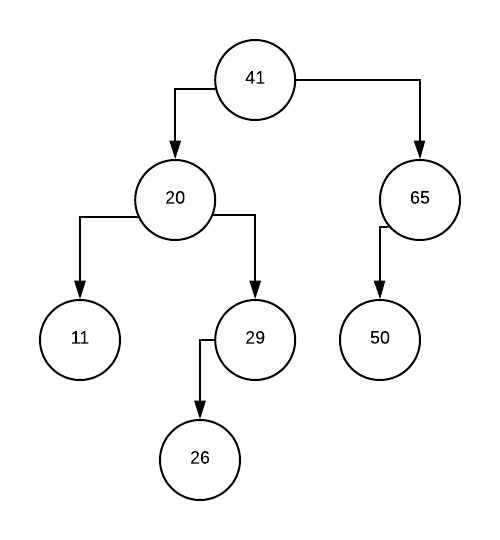
Tree’ga 23 qo’shamiz. Dastlab qo’shish uchun kerakli pozitsiya topiladi, so’ngra element qo’shiladi.
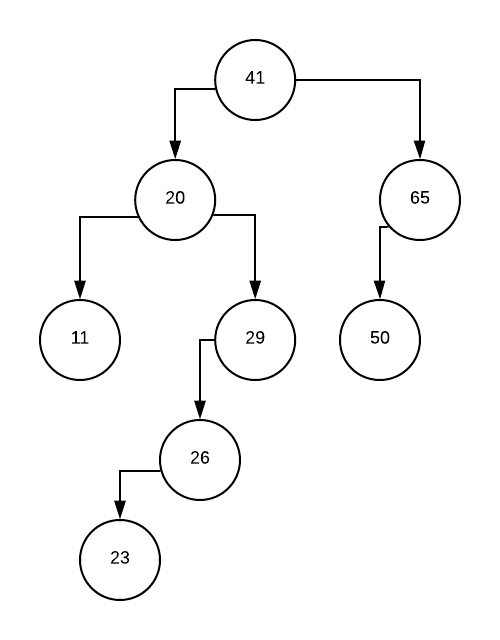
Tree’da balans yo’qoldi, sababi 29 node’ning chap child’i uzunligi 2, o’ng child’i 0. 2 – 0 > 1. Balansni to’g’rilash uchun 29 node’ni o’ngga buramiz. Shunda 26 parent bo’lib qoladi, uning chap child’i – 23, o’ng child’i 29 bo’ladi.
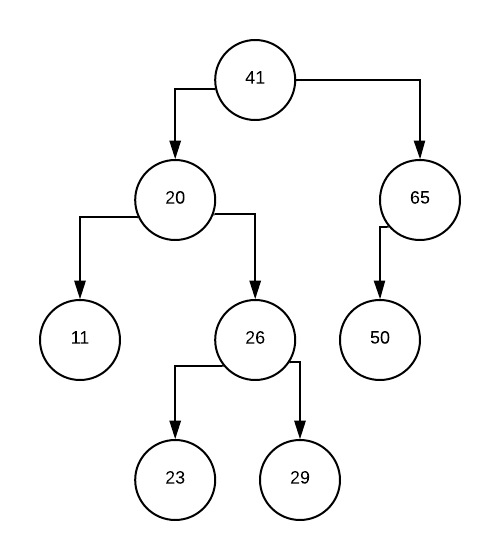
Tree’ga balans qaytdi.
Yana bir misol. Tree’ga 55 qo’shamiz.
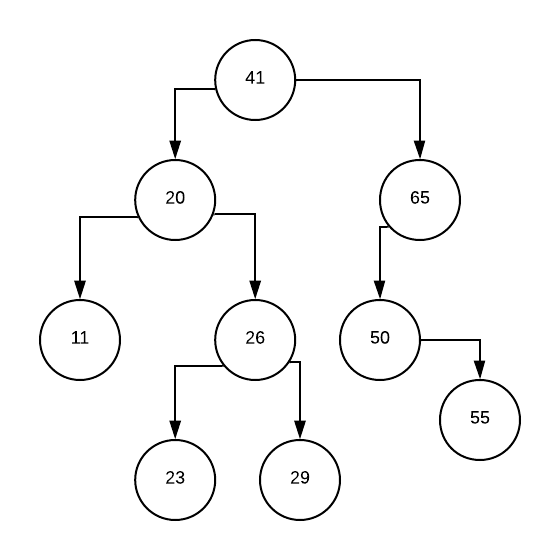
Endi 65 node’ning chap child’ining uzunligi – 2, o’ng child’niki – 0. E’tiborlisi – endi bitta burish bilan balansga keltira olmaymiz, yana bir urinish kerak bo’ladi.
50 node’ni chapga buramiz, 55 parent bo’lib qoladi:
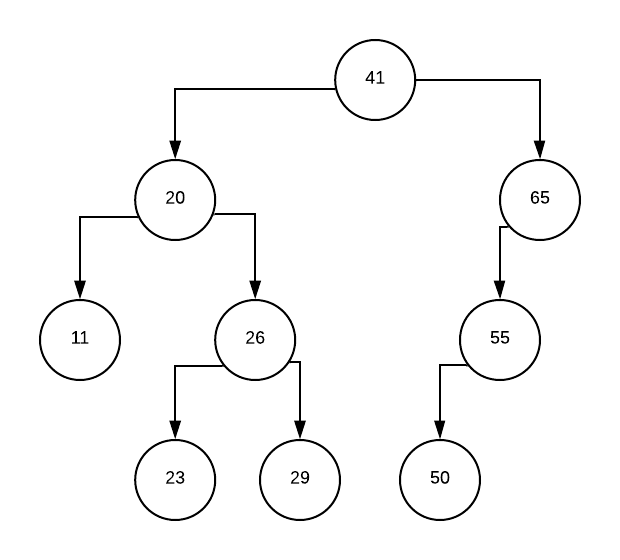
Endi 55 ning parent’i – 65ni o’ngga buramiz. Daraxtga yana balans qaytdi:
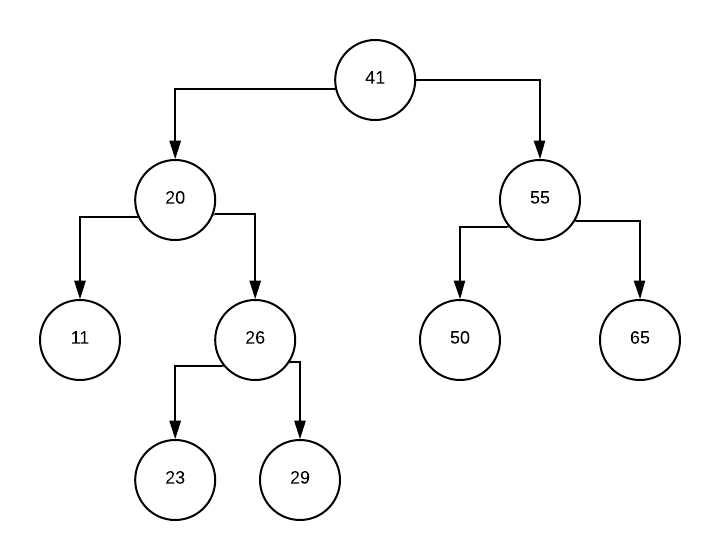
Demak, AVL-tree’ni balansini to’g’rilash uchun bizga bir yoki ikki burish kerak bo’larkan.
Burishlardan xulosa qilib, burish qoidasini umumlashtiramiz:
- node’ning chap tarafi uzun (og’ir) – > 1:
– uning chap child’ining chap child’i bor – node’ni o’ngga buramiz.
– uning chap child’ining o’ng child’i bor – node’ning chap childi’ni chapga buramiz, node’ni o’ngga buramiz
- node’ning o’ng tarafi uzun (og’ir) – > 1:
– uning o’ng child’ining o’ng child’i bor – node’ni chapga buramiz.
– uning o’ng child’ining chap child’i bor – node’ning o’ng childi’ni o’ngga buramiz, node’ni chapga buramiz
O’chirish (Deletion)
O’chirishda ham ikki qadam – node’ni o’chiramiz va balansni qaytadan to’g’rilaymiz.
* * *
Keyingi maqolada AVL-tree ustida amallar uchun API yozamiz…