1D range search (one dimension range search, bir o’lchamli oraliq qidiruv) deb, ro’yxatdan berilgan oraliqda yotgan elementlarni topishga aytiladi.

Ro’yxat bir necha xil ko’rinishda ifodalanishi mumkin:
tartiblanmagan array‘da qidirish uchun array’ning har bir elementini tekshirib chiqish kerak bo’ladi – time complexity – O(N). O’z-o’zidan tartiblanmagan array’dan oraliq qidiruvning o’zi mantiqsiz. Tartiblangan array uchun insert – O(1), qo’shish amali tez ishlaydi.
tartiblangan array uchun qidiruv binary search algoritmi asosida amalga oshiriladi. Time complexity – O(log N). Lekin tezkor qidiruvning badali arrayga malumot qo’shishda toʻlanadi. Maʼlumot qoʻshilgach, array yana tartiblanishi kerak boʻladi – O(N).
binary search tree. Biz avvalgi mavzularda oʻtganimiz – binary search tree da qoʻshish va qidirish O(log N) boʻlgani uchun, u samarador ma’lumot tuzilmasi hisoblanadi. Biz 1D range search’ni ham binary search tree’da ifodalaymiz.
1D range search’ni boshlashdan avval, binary search tree’ga oid ba’zi tushunchalarni aniqlashtirib olamiz.
Size (hajm). Tree’dagi node’ning hajmi deb o’zi va o’zidan keyingi node’lar soniga aytiladi.
Rank (daraja). Tree’dagi node’ning darajasi deb undan chap tarafda joylashgan elementlar soniga aytiladi. Boshqachasiga aytganda, tree’ni tartiblangan array’ga o’girganimizda elementning indeksi uning rank’i bo’ladi.
Size va rank’ni biz Binary search tree API ichiga qo’shamiz.
1D range search
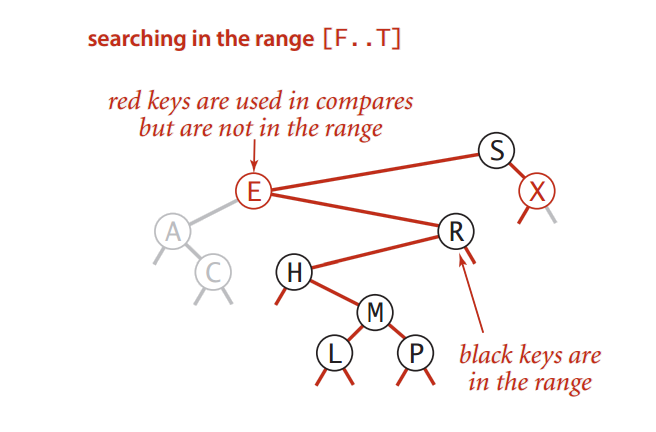
1D search borasida masala ikki xil qo’yilishi mumkin:
- berilgan oraliqda qancha qiymatlar bor?
- berilgan oraliqdagi qiymatlarni topish
Birinchi holatda shunchaki berilgan oraliq chegaralari – low va high qiymatlarining rankini topib high’dan low’ni ayiramiz. Nimaga ayiramiz? Sababi, high’ning ranki ichida low va uning child’larining soni ham bo’ladi. Ayirish bilan low chegaradan kichkina qiymatlar sonini high rank’dan chiqarib tashlaymiz.
Agar high qiymat tree’da bo’lsa, u holda qiymatlar soniga high chegarani ham qo’shamiz, +1.
Berilgan oraliqdagi qiymatlarni topish uchun rekursiya ichida oraliqdagi qiymatlarni ko’rib chiqib, ularni arrayga yig’amiz.
Tahlil
Time complexity – O(R + h). Bunda R topilgan elementlar soni, eng yomon holatda tree’dagi elementlar soni – N ga teng. h – daraxtning uzunligi. Tree’ balanslangan bo’lganda, h = Log N bo’ladi.
* * *
Kod Githubda: https://github.com/Webmaxor/leetcode-solutions/blob/master/algorithms/trees/binary-search-trees.js
* * *
Mavzu bo’yicha savollarni Github’dagi Webmaxor / leetcode-solutions repository’da yozishingiz yoki kodda Reference in new issue ni bosib, qoldirishingiz mumkin.