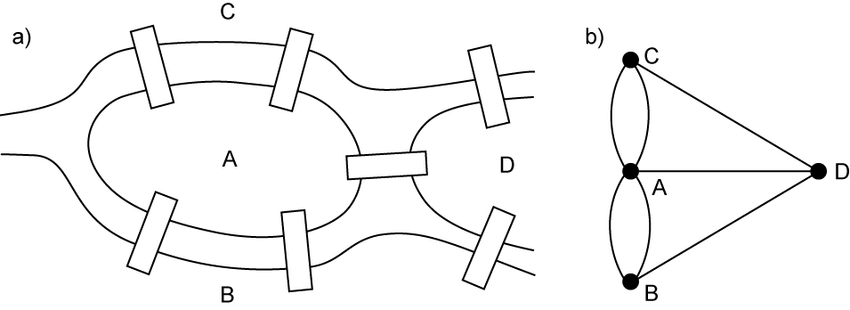
Kenigsberg (Königsberg, hozirgi Kaliningrad) shahridagi yetti ko’prikni qanday qilib bir ko’prikga ikki marta chiqmasdan bosib o’tish – qadimiy matematik masalalardan biri bo’lib, birinchi marta 1736-yilda Leonard Eyler tomonidan yechilgan. Eyler har bir ko’prikdan faqat bir marta foydalanib barcha ko’priklarni aylanib chiqish imkonsizligini isbotlab bergan.

U daryo kesib o’tgan quruqliklarni vertex, ko’priklarni – edge deb hisoblab, muammoning graph’ini hosil qilgan. Masalani graph‘ga moslashtirganda, qo’yiladigan shart – barcha edge’larni faqat bir martadan bosib o’tish imkonini beradigan cycle bormi, savolini qo’ygan.
Izlanishlardan so’ng, Eyler graph nazariyasining birinchi teoremasi – agar vertex’lar bog’langan va vertex’lardagi bog’lanishlar soni (degree) juft bo’lsa, albatta imkoni bor, degan xulosaga kelgan.
Shuningdek, yana bir nechta qiziq xulosalarni taqdim etgan:
1. Graph’dagi toq darajali (degree) vertex’lar miqdori juft son bo’lishi kerak. Toq darajali, toq miqdordagi vertex’lardan o’zaro bog’langan graph yasab bo’lmaydi.
2. Eulerian cycle. Agar graph’ning barcha vertex’lari o’zaro bog’langan va juft darajali bo’lsa, u holda har bir edge’ni faqat bir marta bosib o’tgan holda boshlang’ich nuqtaga qaytib kelish mumkin (cycle, birinchi teorema).
Aylana (cycle) bo’lishi uchun, boshlangan joyga – birinchi vertex’ga qaytib kelish kerak bo’ladi. Demak, har bir vertex’ga kirish va undan chiqish uchun vertex’da kamida ikki va undan ko’p juft miqdordagi edge’lar bo’lishi zarur.
3. Eulerian path. Agar graph’ning ikki vertex’i toq darajali bo’lsa, har bir edge’ni faqat bir marta bosib o’tish mumkin, lekin aylana qilib bo’lmaydi. Boshlang’ich nuqtani birinchi toq vertex’dan boshlab, ikkinchi toq vertex’da tugatish kerak.
Kenigsberg ko’prigi masalasini yechishning imkoni yo’qligi sababi – vertex’larning barcha edge’lari miqdori – toq son. Agar yana bitta ko’prik qo’shilsa, ikkita vertex toq daraja, qolgan ikkitasi juft darajaga keladi. Shunda barcha ko’priklarga bir martadan chiqqan holda barcha ko’priklarni aylanib chiqish mumkin.
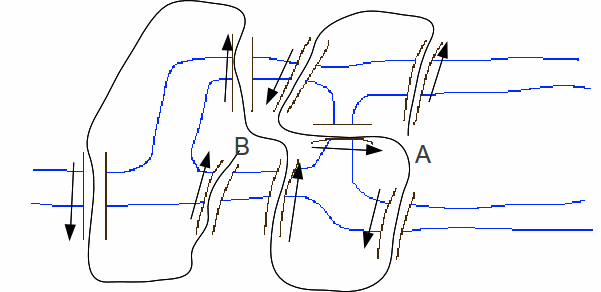
4. Ikkitadan ortiq toq darajali vertex bo’lsa, u holda barcha edge’larni bir martadan bosib o’tish imkonsiz.
Masalalar
Masala 1. Graph’ni Eulerian cycle’ga tekshiramiz.
Ishlash tartibi. Depth first search yordamida vertex’larni «ko’rilgan» (marked) qilib belgilab chiqamiz. Bunda ko’rilayotgan har bir vertex’ning degree’sini (edge’lari sonini) tekshiramiz. Agar degree toq son bo’lsa, DFS ishini tugatamiz. DFS barcha vertex’larni ko’rilgan qilib belgilab chiqmagan bo’lsa, demak graph – Eulerian cycle emas.
* * *
Masala 2. Graph’ning Eulerian path’ga tekshiramiz.
Ishlash tartibi. Depth first search yordamida vertex’larni «ko’rilgan» (marked) qilib belgilab chiqamiz. Bunda ko’rilayotgan har bir vertex’ning degree’sini (edge’lari sonini) tekshiramiz. Agar ikkitadan ortiq vertex’ning degree’si toq son bo’lsa, DFS ishini tugatamiz. DFS barcha vertex’larni ko’rilgan qilib belgilab chiqmagan bo’lsa, demak graph – Eulerian path emas.
* * *
Masala 3. Biz Eyler aylanalaridan xulosa qilib, graph’da har bir edge’larni bir martadan bosib o’tgan holda aylana qlish mumkinligini ko’rib o’tamiz.
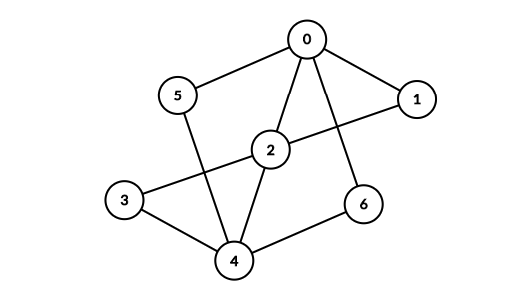
Ishlash tartibi. Agar 0 dan boshlasak, 0 – 1 – 2 – 3 – 4 – 2 – 0 – 6 – 4 – 5 – 0 cycle hosil qilish mumkin. Albatta dastur bizga aynan shu ketma-ketlikni kafolatlamaydi. Path yasashni depth first search yordamida bajaramiz, farqi biz endi vertex’larni emas, edge’larni marked qilib belgilaymiz (Har bir edge’ni faqat bir marta ishlatish mumkin bo’lgani uchun).