Biz o’tgan graph masalalarida asosan undirected graph‘larni ko’rib chiqdik. Aslida undirected graph directed graph‘dan kodda ifodalanganda bor yo’g’i graph’dagi barcha vertex’larning ikki tomonlama (ikki yo’nalishli) bog’langani bilan farq qiladi. Shuning uchun undirected graph masalalaridagi yechimlar yoki algoritmlar direct graph uchun ham mos kelishi mumkin. Masalan, biz depth first search yoki breadth first search‘ni ikki turdagi graph uchun ham qo’llay olamiz.
Leetcode‘ning ba’zi masalalari, garchi shartida ko’rsatib o’tilmagan bo’lsada, aynan directed graph ma’lumotlar tuzilmasini qo’llashni taqozo qiladi. Misol uchun, 207. Course Schedule masalasida o’quv kurslariga qatnashish ketma-ketligi haqida gap borgan:
There are a total of numCourses courses you have to take, labeled from 0 to numCourses-1.
Some courses may have prerequisites, for example to take course 0 you have to first take course 1, which is expressed as a pair: [0,1]
Given the total number of courses and a list of prerequisite pairs, is it possible for you to finish all courses?
Osonroq tushuntiradigan bo’lsak, 0-kursni (geometriya) boshlash uchun, avval 1-kursni (arifmetika) tugatish kerak bo’ladi. [0, 1] ni 1 -> 0 graph’ga aylantiramiz va 1 dan boshlab, 0 da tugata olamiz.
[ [0, 1] ] – bu yerda edge list.
Agar berilgan kurslar ketma-ketligi [ [ 0, 1], [1, 0] ] holatida bo’lsa, 1->0, 0 -> 1 – aylana (cycle) bo’lib qoladi. Kurslarni tugatish uchun esa, berilgan ketma-ketlikdagi kurslar aylana bo’lmasligi kerak.
Ok, yana ham tushunarli bo’lishi uchun kurslarni ko’paytiraylik. Chunki masaladagi bir-ikki edge umumiy mavzuni ochib berolmayapti.
Bizda quyidagi o’quv kurslari bor:
0. Algorithms
1. Complexity theory
2. Artificial Intelligence
3. Intro to Computer Science
4. Cryptography
5. Scientific Computing
6. Advanced programming.
Biz ularni sanoq tartibida o’rganishni boshlay olmaymiz, o’rganish ketma-ketligi sanoq tartibida emas . Masalan, «0. Algorithms»ni boshlash uchun «6. Advanced programming» ni tugatish kerak. Ketma-ketlik graph ko’rinishida ifodalangan:
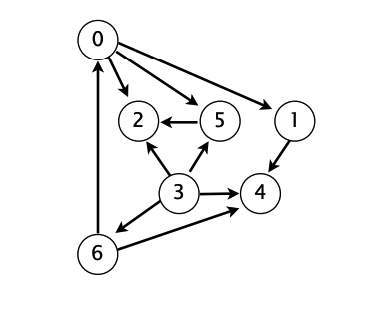
Masalani yechish uchun, birinchi navbatda, graph’ni cycle’ga tekshirishimiz kerak bo’ladi. Sababi, cycle bo’lgan holatda biz kurslarni tugata olmay qolamiz.
Cycle bo’lmagan graph’larni Directed Acyclic Graph (DAG) deyiladi. DAGning qoidasi – graph’ning istalgan vertex’idan depth first search‘ni boshlaganimizda edge’lar ketma-ketligi boshlang’ich vertex’ga kelmasligi kerak.
DAG graph – yuqoridagi kabi scheduling (ketma-ketlik, rejalashtirish) tipidagi masalalarni yechish uchun ayni muddao. Lekin baribir graph’dan ketma-ketlikni topishimiz kerak, qaysi kursni birinchi bo’lib boshlash uchun. To’g’rirog’i, kodimiz ishlab, birga qayerdan (qaysi vertex’dan) boshlashni aniqlashtirib bersin. DAG graph’ning qayeridan boshlashni aniqlash usuli – topological sort deyiladi.
Topological sort
Topological sort algoritmi bizga graph’dagi vertex’larni edge’larning yo’nalishi bo’yicha tekshirib maxsus tartiblab beradi. Topological sort sanoq tartibida tartiblamaydi. Topological sort’dagi muhim fakt – biz qidirayotgan yoki ko’rmoqchi bo’lgan vertex’ga faqat unga bog’langan vertex’larni ko’rib chiqibgina kela olamiz. Masalan, quyidagi graph’da biz 2 ga faqat 0 va 4 ni ko’rib chiqqach, kelishimiz mumkin. O’z navbatida 0 va 4 ni ko’rish uchun avval 1 ga kirish kerak.
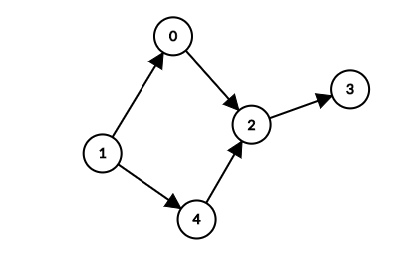
Graph’da ikki yo’l mavjud 1 -> 0 -> 2 -> 3 va 1 -> 4 -> 2 -> 3. Agar biz vertex’larni shu tartiblardan birida o’qib oladigan bo’lsak, bu topologik tartiblash – topological sort bo’ladi. Topological sort uchun ham depth first search algoritmidan foydalanamiz.
Endi yuqoridagi o’quv kurslari misoliga qaytadigan bo’lsak, kurslar ketma-ketligi topological sort’da quyidagicha bo’ladi:
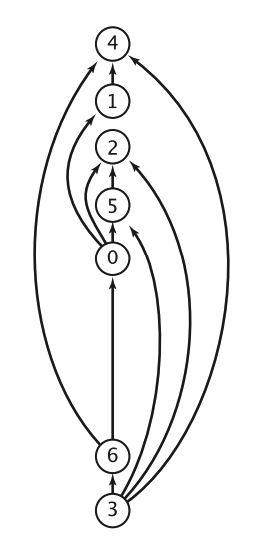
Demak barcha kurslarni tugatish uchun, avval «3. Intro to Computer Science» dan boshlash kerak bo’larkan.
Kod
* * *
207. Course Schedule masalani ishlash tartibi
- Masaladagidagi «prequisite» juftlarini edge’lar deb olib, ular asosida adjacency list graph shakllantiramiz.
- Depth first search’da graph’ni tekshiramiz. Bu yerda cycle’ni aniqlash muhim, shunda kursni yakunlash mumkin bo’lmay qoladi. Cycle’ni aniqlash uchun vertex’ni tekshirishda, avvalgi kodlarda foydalanganimiz marked o’rniga
checking[]vachecked[]‘ni ishlatamiz. - DFS ishini boshlaganda vertex’ni
checking[vertex] = trueqilib belgilaymiz. Edgelarini tekshirib bo’lgach,checking[vertex] = falsevachecked[vertex] = truega o’zgaradi. Agarchecking[vertex] = truepaytida DFS yana shu vertex’ni tekshirishga kirsa, demak cycle aniqlangan bo’ladi.