Dijkstra’ning algoritmi graph‘dagi bir vertex’dan boshqa har bir vertex’ga qisqa yo’lni topish uchun ishlatiladi.
Algoritm boshlang’ich vertex’dan boshlab, barcha bog’langan vertex’larni tekshirib chiqmaguncha ishni davom ettiradi. Demak, biz Dijkstra algoritmini bir marta qo’llab, natijalarni biror yerda (arrayda) saqlab qo’yishimiz, zarur holda boshlang’ich vertex’dan boshqa bir vertex’ga qisqa yo’lni topish kerak bo’lganda, natijani O(1) vaqt ichida saqlangan joydan o’qib olishimiz mumkin. Agar boshlanish nuqtasi sifatida boshqa vertex tanlansa, Dijkstra algoritmini yana bir marta ishga tushirishimiz kerak bo’ladi.
Dijkstra algoritmi
Algoritmning umumiy qoidalari quyidagicha:
- Har safar vertex’ni tekshirmoqchi bo’lganimizda, doim weight’i kichkina edge’li vertex’ni tanlaymiz.
- Vertex’ga kelganimizda, uning qo’shni vertex’larini tekshiramiz.
- Har bir qo’shni vertex uchun, boshlang’ich node’dan qo’shni node’gacha bo’lgan edge weight’lari yig’indisini hisoblab chiqamiz.
- Agar qo’shni node’ga hisoblangan weight yig’indisi undagi bor qiymatdan kichik bo’lsa, uninq qiymatini yangilaymiz (edge relaxation).
Ishlash tartibini misolda ko’rib chiqamiz. Bizda quyidagi graph bor.
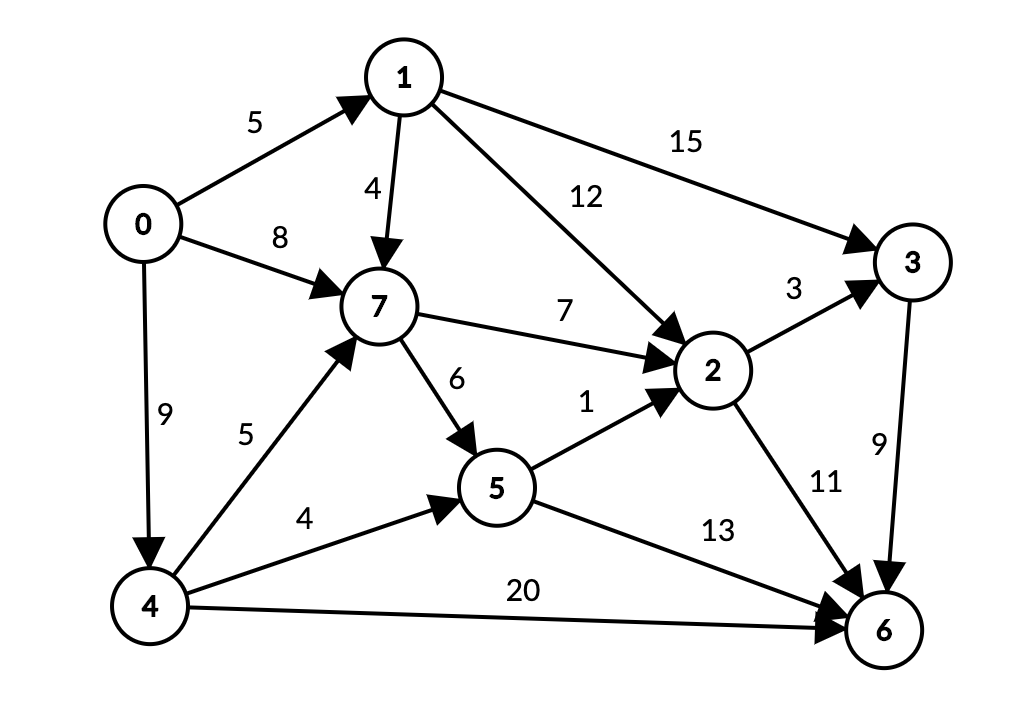
Tekshirishni 0 vertex’dan boshlaymiz. Tekshirish davomida boshlang’ich vertex’dan boshqa vertex’larga masofalarni distTo[] ga yig’amiz. Masofa deb aytdim, aslida masofa o’lchovi edge weightlarining yig’indisi hisoblanadi.
0 dan 1, 7 va 4 vertex’larga edge bor. Ular uchun 0 vertex’dan masofani hisoblaymiz.
| v | distTo | edgeTo |
|---|---|---|
| 0 | 0 | – |
| 1 | 5 | 0 |
| 2 | – | |
| 3 | – | |
| 4 | 9 | 0 |
| 5 | – | |
| 6 | – | |
| 7 | 8 | 0 |
0 dan unga bog’langan vertex’lardagi eng kichik masofa – 5, u 1 vertexda. 1 vertexdan davom ettiramiz.
1 dan 3, 2, 7 vertex’ga masofa bor. Ular uchun boshlang’ich nuqta – 0 vertex’dan masofani hisoblaymiz.
| v | distTo[] | edgeTo[] |
|---|---|---|
| 0 | 0 | – |
| 1 | 5 | 0 |
| 2 | 5 + 12 = 17 | 1 |
| 3 | 5 + 17 = 20 | 1 |
| 4 | 9 | 0 |
| 5 | – | |
| 6 | – | |
| 7 | 8 | 0 |
0 -> 1 -> 7 masofasi = 9 chiqdi. Bizdagi 0 -> 7 masofa kichikroq – 8 ga teng. Shuning uchun 7 ga masofani yangilamaymiz. Faqat yangi masofa eskisidan kichik bo’lgandagina yangilanadi Bu kabi yangilashni edge relaxation deyiladi.
1 ni tekshirib bo’lganimiz uchun unga boshqa qaytmaymiz.
distTo qiymatlariga ko’ra, navbatdagi kichik masofa 7-vertex’da. 7-vertex’dan tekshirishni davom ettiramiz.
7 dan 2 va 5 ga edge bor. Ular uchun boshlang’ich nuqta – 0 vertex’dan masofani hisoblaymiz.
| v | distTo | edgeTo |
|---|---|---|
| 0 | 0 | – |
| 1 | 5 | 0 |
| 2 | 7 | |
| 3 | 5 + 17 = 20 | 1 |
| 4 | 9 | 0 |
| 5 | 8 + 6 = 14 | 7 |
| 6 | – | |
| 7 | 8 | 0 |
2-vertex’ning masofasi yangilandi, sababi 0 -> 1 -> 2 dan ko’ra 0 -> 7 -> 2 yaqinroq ekan. 5 ga esa yangi qiymat qo’shildi (edge relaxation).
Navbatdagi kichik masofa – 4-vertexda. 4-vertex’dan tekshirishni davom ettiramiz.
4 dan 5, 6, 7 ga edge bor. Ular uchun boshlang’ich nuqta – 0 vertex’dan masofani hisoblaymiz.
| v | distTo | edgeTo |
|---|---|---|
| 0 | 0 | – |
| 1 | 5 | 0 |
| 2 | 7 | |
| 3 | 5 + 17 = 20 | 1 |
| 4 | 9 | 0 |
| 5 | 4 | |
| 6 | 9 + 20 = 29 | 4 |
| 7 | 8 | 0 |
0 -> 7 -> 5 masofasi 14 ga teng edi, 0 -> 4 -> 5 = 13 chiqdi, demak 5-vertex uchun distTo dagi qiymatni yangilaymiz.
6 bo’sh edi, unga yangi qiymat 29 qo’shildi.
7-vertex’ga yo’l – 0 -> 4 -> 7 masofasi 14, bor qiymat 8 dan kichik. 7-vertex’ning masofasi 8 ligicha qoladi.
Navbadagi kichik masofa 5-vertex’da. 5-vertex’dan tekshirishni davom ettiramiz.
5 dan 2 va 6 ga edge bor. Ular uchun boshlang’ich nuqta – 0 vertex’dan masofani hisoblaymiz.
| v | distTo | edgeTo |
|---|---|---|
| 0 | 0 | – |
| 1 | 5 | 0 |
| 2 | 5 | |
| 3 | 5 + 17 = 20 | 1 |
| 4 | 9 | 0 |
| 5 | 4 | |
| 6 | 4 | |
| 7 | 8 | 0 |
0 dan 2 gacha masofa ( 0 -> 4 -> 5 -> 2 ) 9 + 4 + 1 = 14 ga teng. 14 hozirgi qiymat 15 dan kichkina. 2 ning masofasini yangilaymiz (edge relaxation).
0 dan 6 gacha masofa ( 0 -> 4 -> 5 -> 6 ) 9 + 4 + 13 = 26 ga teng. 26 hozirgi qiymat 29 dan kichik. 6 ning masofasini yangilaymiz (edge relaxation).
Navbadagi kichik masofa 2-vertex’da. 2-vertex’dan tekshirishni davom ettiramiz.
2 dan 3 va 6 ga edge bor. Ular uchun boshlang’ich nuqta – 0 vertex’dan masofani hisoblaymiz.
| v | distTo | edgeTo |
|---|---|---|
| 0 | 0 | – |
| 1 | 5 | 0 |
| 2 | 5 | |
| 3 | 2 | |
| 4 | 9 | 0 |
| 5 | 4 | |
| 6 | 2 | |
| 7 | 8 | 0 |
0 dan 3 gacha masofa ( 0 -> 4 -> 5 -> 2 -> 3 ) 9 + 4 + 1 + 3 = 17 ga teng. 17 hozirgi qiymat 20 dan kichkina. 3 ning masofasini yangilaymiz. (edge relaxation).
0 dan 6 gacha masofa ( 0 -> 4 -> 5 -> 2 -> 6 ) 9 + 4 + 1 + 11 = 25 ga teng. 25 hozirgi qiymat 26 dan kichkina. 6 ning masofasini yangilaymiz. (edge relaxation).
Navbadagi kichik masofa 3-vertex’da. 3-vertex’dan tekshirishni davom ettiramiz.
3-vertex’da faqat bitta edge bor – 6-vertex’ga. 6 uchun boshlang’ich nuqta – 0 vertex’dan masofani hisoblaymiz.
| v | distTo | edgeTo |
|---|---|---|
| 0 | 0 | – |
| 1 | 5 | 0 |
| 2 | 5 | |
| 3 | 2 | |
| 4 | 9 | 0 |
| 5 | 4 | |
| 6 | 2 | |
| 7 | 8 | 0 |
0 dan 6 gacha masofa ( 0 -> 4 -> 5 -> 2 -> 3 -> 6 ) 9 + 4 + 1 + 3 + 9 = 26 ga teng. 26 hozirgi qiymat 25 dan katta. 6 ning masofasio’zgarmaydi.
Navbadagi kichik masofa 6-vertex’da. 6-vertex’dan tekshirishni davom ettiramiz.
6-vertex’ning edge’lari yo’q, demak hisoblashlar tugadi. Yakuniy jadval quyidagicha bo’ladi.
| v | distTo | edgeTo |
|---|---|---|
| 0 | 0 | – |
| 1 | 5 | 0 |
| 2 | 14 | 5 |
| 3 | 17 | 2 |
| 4 | 9 | 0 |
| 5 | 13 | 4 |
| 6 | 25 | 2 |
| 7 | 8 | 0 |
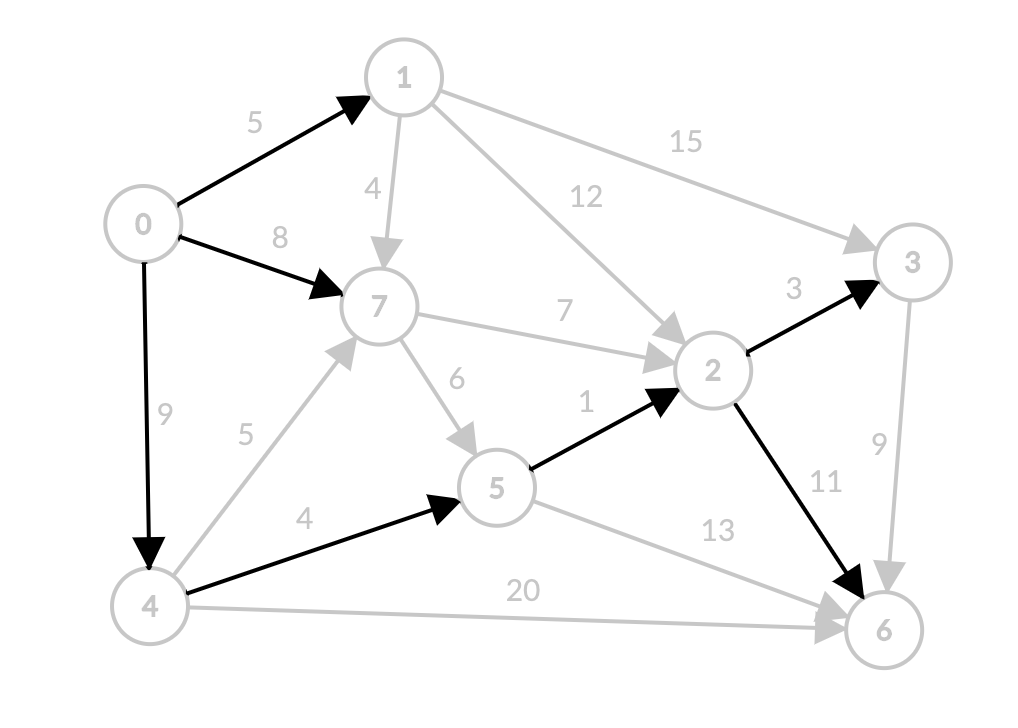
edgeTo ma’lumotlari asosida path’larni yig’adigan bo’lsak qisqa path’lar quyidagicha bo’ladi:
- 0 dan 1 gacha: 0->1
- 0 dan 2 gacha: 0 -> 4 -> 5 -> 2
- 0 dan 3 gacha: 0 -> 4 -> 5 -> 2-> 3
- 0 dan 4 gacha: 0-> 4
- 0 dan 5 gacha: 0 -> 4 -> 5
- 0 dan 6 gacha: 0 -> 4 -> 5 -> 2-> 6
- 0 dan 7 gacha: 0 -> 7
Kod
Kod Githubda: https://github.com/Webmaxor/leetcode-solutions/blob/master/algorithms/graphs/shortest-path/dijkstra-shortest-path.js
* * *
Mavzu bo’yicha savollarni Github’dagi Webmaxor / leetcode-solutions repository’da yozishingiz yoki kodda Reference in new issue ni bosib, qoldirishingiz mumkin.