Ushbu maqolada biz negativ (manfiy) weight’larning graph‘da shortest path‘ni topishdagi ta’sirini ko’rib chiqamiz. Avvaldan aytib o’tish kerakki, negativ weight’lari bor graph’lar uchun bir ko’rib o’tgan Dijkstra algoritmi ishlamaydi.
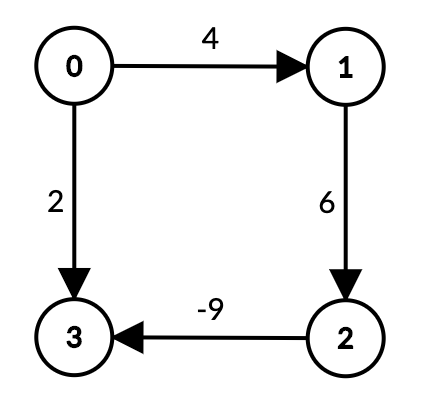
Ushbu graph’da 0 vertex’dan 3 ga qisqa yo’lni topish uchun Dijkstra’ning shortest path algoritmini qo’llasak, u 0 -> 3 (2) ni qaytaradi. Aslida shortest path 0 -> 1 -> 2 -> 3 (4 + 6 + (-9) = 1) bo’lishi kerak edi.
Re-weighting, ya’ni har bir edge weight’ga bir xil son qo’shib, weightlarni pozitiv (>=0) qilib oladigan bo’lsak, shortest path 0 -> 3 bo’lib qoladi. Shortest path’ning o’zgarib qolishi – noto’g’ri yechim.
Topological sort negativ weight’larda ham to’g’ri ishlaydi, faqat buning uchun graph acyclic (DAG) bo’lishi kerak. Demak bizdagi masala – aylana bo’lishi mumkin bo’lgan negativ weight’li graph’larda shortest path’ni topish kerak.
Negativ aylanalar
Negativ aylanalar (negative cycles) deb, weight’lar yig’indisi manfiy son chiqadigan aylanalarga aytiladi. Tabiiyki, negative aylanalarda shortest path’ni topish imkonsiz, algoritm negativ aylana ichida cheksiz aylanib yuradi. Masalan quyidagi graph’da, 0 dan 6 gacha shortest path’ni topishda, 4 -> 7 -> 5 (0.37 + 0.28 + (-0.66) = -0.01) negativ aylana ichida aylanib yuradi.
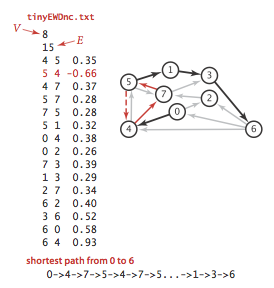
Demak, graph’da negativ weight’li edge’lar bo’lsa, shortest path’ni topishdan avval, graph’da negativ aylanalar bor-yo’qligini aniqlash kerak bo’ladi. Yo’q bo’lsa, shortest path’ni topish mumkin.
Bellman-Ford algoritmi
Algoritmga ko’ra, agar graph’da V sondagi vertex’lar bo’lsa, V marta barcha edge’larni relax qilib chiqish kerak. Bo’ldi. Shu tariqa, algoritm negativ cycle bo’lmagan graph’da shortest path’larni topadi.
for (let pass = 0; pass < graph.length; pass++) {
for (let v = 0; v < graph.length; v++) {
graph[v].forEach(edge => relax(edge))
}
}
Nima uchun V marta?
Nima uchun effektiv bo’lmagan algoritmni ishlatishga majbur bo’layotganimizni yuqorida tushuntirib o’tdim: biz negativ weight’lar uchun Dijkstra algoritmini qo’llay olmaymiz; graph’da aylana bo’lsa topological sort algoritmi ham ishlamaydi. Qisqasi, bizda tanlov ko’p emas.
Biz vertex’larni ketma-ketlikda ko’rib chiqar ekanmiz, boshlang’ich nuqtadan shortest path birinchi siklda (pass = 0) optimal bo’lmaydi. Barcha optimal shortest path’larni topganimizga ishonch hosil qilish uchun, har bir vertex’ni V marta tekshirishimiz kerak.
Quyidagi graph bilan tanishsiz, undan avvalgi shortest path maqolalarida ham foydalanyapmiz.
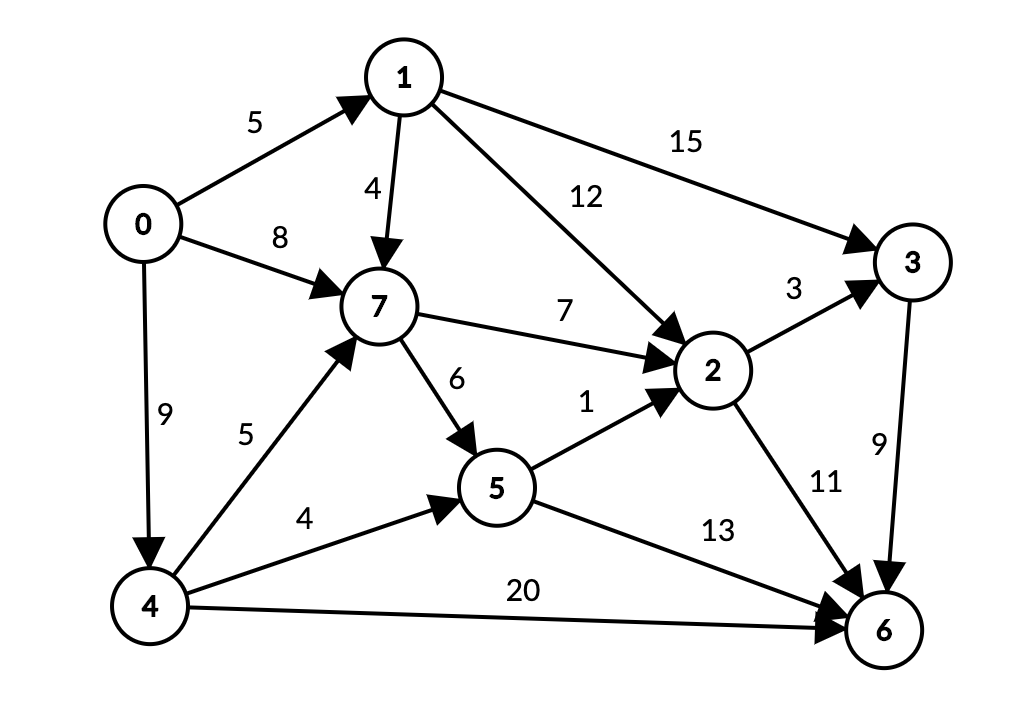
Ushbu graph’ga Bellman-Ford algoritmini qo’llaymiz.
Biz har bir vertex uchun edge relaxation amalini qo’llab chiqamiz. Masofa va bog’lanishlarni odatdagidek distTo[] hamda edgeTo[] ga yig’ib boramiz.
Birinchi siklni boshlaymiz (pass=0).
Graph’dagi vertex’lar tartibiga ko’ra, tekshirishni 0-vertex’dan boshlaymiz. 0 dan 1, 7 va 4 vertex’larga edge bor. Ular uchun 0 vertex’dan masofani hisoblaymiz.
| v | distTo | edgeTo |
|---|---|---|
| 0 | 0 | – |
| 1 | 5 | 0 |
| 2 | – | |
| 3 | – | |
| 4 | 9 | 0 |
| 5 | – | |
| 6 | – | |
| 7 | 8 | 0 |
1-vertexdan davom ettiramiz.
1 dan 3, 2, 7 vertex’ga edge bor. Ular uchun boshlang’ich nuqta – 0 vertex’dan masofani hisoblaymiz.
| v | distTo[] | edgeTo[] |
|---|---|---|
| 0 | 0 | – |
| 1 | 5 | 0 |
| 2 | 5 + 12 = 17 | 1 |
| 3 | 5 + 17 = 20 | 1 |
| 4 | 9 | 0 |
| 5 | – | |
| 6 | – | |
| 7 | 8 | 0 |
2-vertexdan davom ettiramiz.
2 dan 3 va 6 vertex’ga edge bor. Ular uchun boshlang’ich nuqta – 0 vertex’dan masofani hisoblaymiz.
| v | distTo[] | edgeTo[] |
|---|---|---|
| 0 | 0 | – |
| 1 | 5 | 0 |
| 2 | 17 | 1 |
| 3 | 20 | 1 |
| 4 | 9 | 0 |
| 5 | – | |
| 6 | 17 + 11 = 28 | 2 |
| 7 | 8 | 0 |
0 -> 1 -> 2 -> 3 masofasi 5 + 12 + 3 = 20 chiqdi. 0 -> 1 -> masofasi ham 20 (5 + 15). Shuning uchun 3 masofasi o’zgarmaydi. 0 -> 1 -> 2 -> 6 masofasi 28 ga teng.
3-vertexdan davom ettiramiz.
3 dan 6 vertex’ga edge bor. 6 uchun boshlang’ich nuqta – 0 vertex’dan masofani hisoblaymiz: 0 -> 1 -> 3 -> 6 masofasi 5 + 15 + 9 = 29. Bizdagi masofa 28 kichikroq, shuning uchun jadvalda hech narsa o’zgarmaydi.
| v | distTo[] | edgeTo[] |
|---|---|---|
| 0 | 0 | – |
| 1 | 5 | 0 |
| 2 | 17 | 1 |
| 3 | 20 | 1 |
| 4 | 9 | 0 |
| 5 | – | |
| 6 | 28 | 2 |
| 7 | 8 | 0 |
4-vertexdan davom ettiramiz.
4 dan 7, 5 va 6 vertex’ga edge bor. Ular uchun boshlang’ich nuqta – 0 vertex’dan masofani hisoblaymiz.
| v | distTo[] | edgeTo[] |
|---|---|---|
| 0 | 0 | – |
| 1 | 5 | 0 |
| 2 | 17 | 1 |
| 3 | 20 | 1 |
| 4 | 9 | 0 |
| 5 | 9 + 4 = 13 | 4 |
| 6 | 28 | 2 |
| 7 | 8 | 0 |
5-vertexdan davom ettiramiz.
5 dan 2 va 6 vertex’ga edge bor. Ular uchun boshlang’ich nuqta – 0 vertex’dan masofani hisoblaymiz.
| v | distTo[] | edgeTo[] |
|---|---|---|
| 0 | 0 | – |
| 1 | 5 | 0 |
| 2 | 5 | |
| 3 | 20 | 1 |
| 4 | 9 | 0 |
| 5 | 13 | 4 |
| 6 | 2 | |
| 7 | 8 | 0 |
6-vertexdan davom ettiramiz. 6 da edge yo’q.
7-vertexdan davom ettiramiz.
7 dan 2 va 5 vertex’ga edge bor. Ular uchun boshlang’ich nuqta – 0 vertex’dan masofani hisoblaymiz.
0 -> 7 -> 2 (15) va 0 -> 7 -> 5 (14) masofalari distTo[] da saqlangan 14 va 13 masofalardan katta, demak hech narsa o’zgarmaydi.
Birinchi sikl (pass = 0) dan keyin jadvalimiz quyidagicha ko’rinishga keldi:
| v | distTo[] | edgeTo[] |
|---|---|---|
| 0 | 0 | – |
| 1 | 5 | 0 |
| 2 | 14 | 5 |
| 3 | 20 | 1 |
| 4 | 9 | 0 |
| 5 | 13 | 4 |
| 6 | 26 | 2 |
| 7 | 8 | 0 |
Jadvalni Dijkstra algoritmi maqolasidagi misol bilan taqqoslasangiz, 3-vertex’ning edgeTo dagi qiymati farq qilyapti. Shuning o’zi, birinchi sikl optimal shortest path’ni topish uchun yetarli bo’lmaganini ko’rsatyapti.
Ikkinchi siklni boshlaymiz (pass=1).
0 va 1-vertex’lar jadvalda o’zgarish qilmaydi.
2-vertex’dan davom ettiramiz. 2 dan 3 va 6 vertex’ga edge bor. Ular uchun boshlang’ich nuqta – 0 vertex’dan masofani hisoblaymiz.
| v | distTo[] | edgeTo[] |
|---|---|---|
| 0 | 0 | – |
| 1 | 5 | 0 |
| 2 | 14 | 5 |
| 3 | 2 | |
| 4 | 9 | 0 |
| 5 | 13 | 4 |
| 6 | 26 | 2 |
| 7 | 8 | 0 |
3-vertex’ning masofasi o’zgardi va jadvalni Dijkstra algoritmi maqolasidagi misol bilan taqqoslaganda, bir xil ko’rinishga keldi.
Albatta algoritm V marta ishlayveradi. Lekin biz algoritmga kichik o’zgarish kiritib, uni optimallashtirishimiz mumkin: Agar distTo[v] i siklda o’zgarmasa, demak distTo[v] i+1 da ham o’zgarmaydi.
Algoritmning ishlash vaqti O(E*V), ammo yuqoridagi shartni kiritadigan bo’lsak, amaliyotda ish ancha tezlashadi (worst case O(E*V) qoladi baribir).
Kod
Kod Githubda: https://github.com/Webmaxor/leetcode-solutions/blob/master/algorithms/graphs/shortest-path/bellman-ford-shortest-path.js
* * *
Mavzu bo’yicha savollarni Github’dagi Webmaxor / leetcode-solutions repository’da yozishingiz yoki kodda Reference in new issue ni bosib, qoldirishingiz mumkin.