Matn ichida qidiruv uchun brute-force yondashuvining kamchiligi – pattern’dagi belgilardan biri qidiruvda mos kelmay qolganda, qidiruvni boshqatdan boshlashi kerak. Shuning uchun worst case O(N*M) bo’lib ketadi. Misol uchun, bizda matn A B A A A A B A A A A A A A A A bo’lsin. Pattern esa BAAAAAAAAA.
Qidiruv jarayoni:
A B A A A A B A A A A A A A A A B A A A A A A A A A B A A A A A A A A A B A A A A A A A A A B A A A A A A A A A B A A A A A A A A A B A A A A A A A A A B A A A A A A A A A
E’tibor bergan bo’lsangiz, ikkinchi siklda patternning 6-belgisi mos kelmay qoldi. Demak biz text’dagi biz ko’rib o’tgan ohirgi 6 belgi BAAAAB ekanini bilamiz. Nima uchun qidiruvni yana boshqatdan boshlashimiz kerak? 3-6 sikllarni tushirib qoldirib, 7-sikldan davom ettirishning imkoni bormi?
Knuth-MorrisPratt (KMP) algoritmi mana shu muammoga yechim sifatida kelib, qidiruvni boshqatdan boshlamaslikning imkonini beradi. U Deterministic Finite Automaton g’oyasiga asoslangan.
Deterministic Finite Automaton
Deterministic finite automaton (DFA) – kompyuter nazariyasida (computer science) abstrakt string qidiruvchi mashina. U holatlarning aniq bir to’plami bo’lib, berilgan (yoki tekshirilayotgan) input qiymatiga qarab, bir holatdan ikkinchi holatga o’tishi mumkin. U asil holatdan boshlanib, ohirgi holatga yetganda tugaydi.
Oson misol bilan tushuntirishga harakat qilaman. Bizda quyidagi ro’yhat bor:
[ 'A', 'AA', 'BAC', 'DBCA', 'AFAB', 'AWAVABBBB', 'ABABAB', 'GAAAA', 'FRBABA', 'AJECB' ]
Biz ular ichidan A dan boshlanadiganlarini topishimiz kerak.
Shart asosida DFAni yasaymiz. Shartga ko’ra, stringning birinchi belgisi A bo’lishi kerak, shunda keyingi belgilarni tekshirishni davom ettiradi. Aks holda dastlabki holatda qoladi.
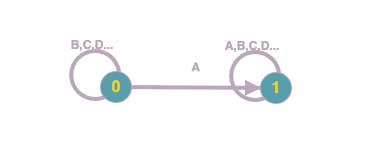
Ro’yhatdan stringlarni tekshirib chiqamiz:
A. 0 holatdan 1 holatga o’tdi. Qidiruv yakunlandi. 1 holatga o’tgani uchun string topilgan hisoblanadi.
AA. A: 0 holatdan 1 holatga o’tdi. A: 1 holatda istalgan belgi bo’lishi mumkin bo’lgani bois, 1 holatda qoldi.
BAC. B: 0 holatda qoldi, sababi 1 holatga faqat birinchi belgi A bo’lgandagina o’tadi.
DBCA. D: 0 holatda qoldi, sababi 1 holatga faqat birinchi belgi A bo’lgandagina o’tadi.
Yana bir misol. ABABAC pattern uchun DFA yasashimiz kerak.
DFA holatlari 0 dan 6gacha bo’ladi. Ideal holatda, ABABAC uchun 6-holatga yetib kela oladi.

Jadval ko’rinishida:
| j | 0 | 1 | 2 | 3 | 4 | 5 |
| pat.charAt(J) | A | B | A | B | A | C |
| A | 1 | 3 | 5 | |||
| B | 2 | 4 | ||||
| C | 6 |
Matnda pattern mos kelmagan holatlardachi?
0-holatdan 1-holatga faqat A bo’lsagina o’tadi. Aks holda 0-holatda qoladi. Demak tekshirilayotgan birinchi belgi B yoki C bo’lsa, birinchi holatda qoladi.
1-holatdan 2-holatga faqat B bo’lsagina o’tadi. Agar A bo’lsa, 1-holatida qoladi, sababi pattern’ga ko’ra, biz uchun birinchi belgi A bo’lishi kerak. C bo’lsa, 0-holatga qaytadi – qidiruv patt[0] dan boshlanadi.
2-holatdan 3-holatga faqat A bo’lsagina o’tadi. Agar B,C bo’lsa, 0-holatga qaytadi.
3-holatdan 4-holatga faqat B bo’lsagina o’tadi. Agar A bo’lsa, 1-holatiga qaytadi; C bo’lsa, 0-holatga qaytadi.
4-holatdan 5-holatga faqat A bo’lsagina o’tadi. Agar B,C bo’lsa, 0-holatga qaytadi.
5-holatdan 6-holatga faqat C bo’lsagina o’tadi. Agar B bo’lsa 4-holatga qaytadi, sababi 5-holatga ko’ra, qidiruvda patternning dastlabki 5 belgisi mos kelgan hisoblanadi, ya’ni qidirilayotgan matnda ABABA allaqachon bor. Keyingi belgi C bo’lishi kerak edi, ammo B chiqdi (ABABAB). Biz avvalgi mos kelgan harflarni bilar ekanmiz, qidiruvni 0-holatdan emas, 4-holatdan, ABABAB holatidan davom ettiramiz. A chiqsa, 1-holatga qaytadi.
6-holatga kelganda qidiruv to’xtaydi, biz matn ichidan patternni topgan bo’lamiz.
Yuqoridagi shartlarni graph ko’rinishida ifodalasak:
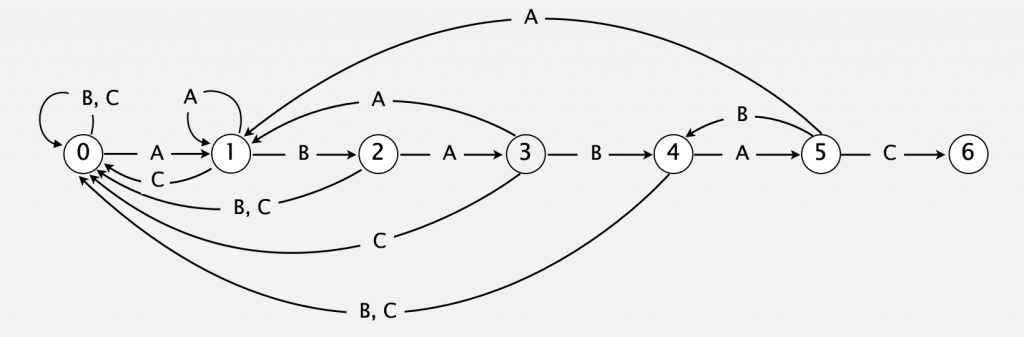
Jadval ko’rinishida:
| j | 0 | 1 | 2 | 3 | 4 | 5 |
| pat.charAt(J) | A | B | A | B | A | C |
| A | 1 | 1 | 3 | 1 | 5 | 1 |
| B | 0 | 2 | 0 | 4 | 0 | 4 |
| C | 0 | 0 | 0 | 0 | 0 | 6 |
Bizda quyidagi matn mavjud: AABACAABABACAA
Pattern esa yuqorida ko’rib o’tganimiz: ABABAC
Matn ichidan patternni topishimiz kerak bo’lsin. Qidiruvni 0-holatdan boshlaymiz.
AABACAABABACAA
1-holatga o’tadi.
AABACAABABACAA
1-holatda qoladi.
AABACAABABACAA
2-holatga o’tadi.
AABACAABABACAA
3-holatga o’tadi.
AABACAABABACAA
0-holatga qaytadi.
AABACAABABACAA
1-holatga o’tadi.
AABACAABABACAA
1-holatda qoladi.
AABACAABABACAA
2-holatga o’tadi.
AABACAABABACAA
3-holatga o’tadi.
AABACAABABACAA
4-holatga o’tadi.
AABACAABABACAA
5-holatga o’tadi.
AABACAABABACAA
6-holatga o’tadi.
Pattern topildi. Qidiruv tugaydi.
Holatlarning o’zgarishini graph va jadvalga qarab boshqatdan ko’rib chiqishingiz mumkin.
Pattern’dan DFAni yasash
Yuqoridagi jadval va graph’ni biz o’zimi ko’rib turib yasadik. Kodda qanday qilib berilgan pattern’dan DFAni yasaymiz?
DFAni yasashda ikki xil holat bor:
Mos kelish. j-holatida, keyingi belgi c == pattern.charAt(j) bo’lsa, u holda j ni bittaga oshiramiz.
Mos kelmaslik. j-holatida, keyingi belgi c != pattern.charAt(j) bo’lsa, u holda ohirgi j-1 belgilar pattern[1..j-1] ichida bo’ladi.
