NFA simulyatsiyasi ishini ko’rib chiqishdan avval NFAning o’zini kodda qanday ifodalanishi bilan tanishib chiqamiz. Avvalgi maqolada aytib o’tilganidek, NFAda 0 dan M gacha state’lar + accept state mavjud. M – bu yerda qavs ichiga olingan regular expression’dagi belgilar soni. Masalan ((A*B|AC)D) regexp uchun NFA state’lari 11 ta (10ta regexp belgi-state + 1 accept state).

NFAning qizil (epsilon) transition’larini esa directed graph ko’rinishida saqlaymiz. Bu bizga state’larni DFSda tekshirib, qaysi path accept state’gacha borishini topish uchun qulayroq yechim. Epsilon transition’lar graph‘da edge ko’rinishida, state’lar vertex ko’rinishida saqlanadi.
0→1, 1→2, 1→6, 2→3, 3→2, 3→4, 5→8, 8→9, 10→11
Qora (match) transition’lar faqat keyingi element’gagina ulanish ehtimoli bo’lgani uchun uni oddiyroq qilib, re[] array’da saqlaymiz. Bunda array elementining indeksi state’ning raqamiga teng bo’ladi. Agar match transition mavjud bo’lsa, o’sha elementning qiymati 1 bo’ladi:
const re = [0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 0]
NFA simulyatsiyasi
NFA simulyatsiyasida abstrakt mashinaning qanday ishlashini misol bilan ko’rib chiqamiz. Regexp o’zgarmagan – ((A*B|AC)D). Biz AABD matnni regexp’ga tekshirishni boshlaymiz.
Siklda dastlab epsilon transition’ga, keyin match transition’ga tekshiriladi.
1. Epsilon transition’da qaysi state’larga yetib borishni tekshiramiz. 0-state’dan 1 ga; 1-state’dan 2 ga va 6 ga; 2-state’dan 3 ga; 3-state’dan 2 ga (2 allaqachon tekshirildi) va 4 ga. Jami 0, 1, 2, 3, 4, 6 state’larga kirdik.
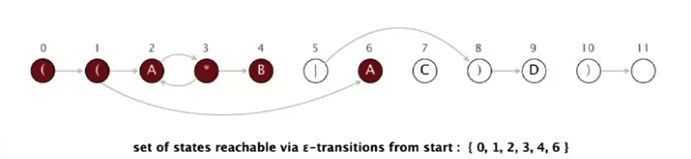
2. Matnning birinchi belgisi A, u 2-va 6-state’da bor. Endi match transition’ni re[] array’dan tekshiramiz. Agar re[2] va re[6] qiymatlari 1 ga teng, ya’ni keyingi state’ga black transition bor. 3 va 7-state’ga o’tamiz. Demak, birinchi A belgini tekshirganimizdan keyin biz 3 va 7 state’ga keldik.
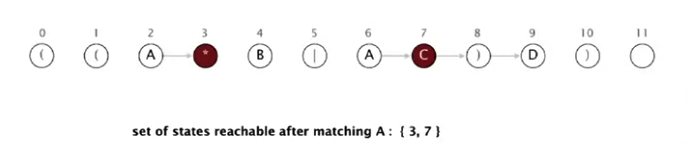
3. 3 va 7 state’dan epsilon transition’ga tekshiramiz. 3 dan 2 ga va 4 ga epsilon transition bor; 2 dan esa 3 ga epsilon transition bor; 7 dan epsilon transition yo’q. Shunday qilib, biz hozir 2, 3, 4 va 7 state’larda turibmiz.
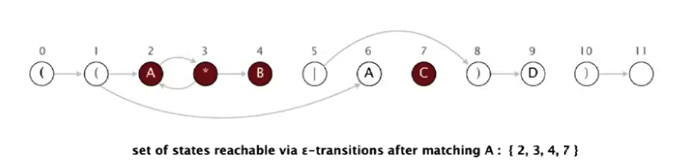
4. Matnning ikkinchi belgisi ham A, u faqat 2-state’da bor. Match transition’ni re[] array’dan tekshiramiz. re[2] qiymati 1 ga teng, ya’ni keyingi state’ga black transition bor. 3-state’ga o’tamiz. AA ni tekshirganimizdan keyin biz 3-state’da turibmiz.
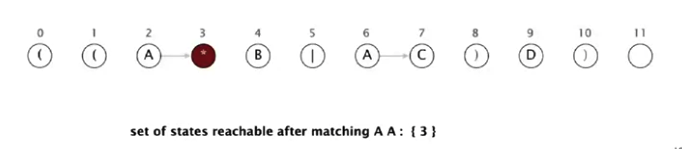
5. 3-state’dan epsilon transition’ga tekshiramiz. 3 dan 2 ga va 4 ga epsilon transition bor. 2 dan esa 3 ga epsilon transition bor; Biz hozir 2, 3, 4 state’da turibmiz.
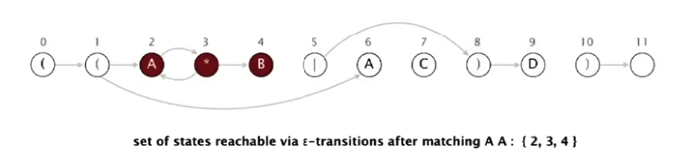
6. Uchinchi belgi – B faqat 4-state’da mavjud. Undan 5 ga match (black) transition bor. 5-state’ga o’tamiz. AAB ni tekshirganimizdan keyin biz 5-state’da turibmiz.
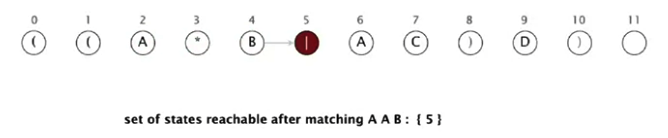
7. 5-state’dan 8 ga epsilon transition bor; 8 dan 9 ga epsilon transition bor. Hozir biz 5, 8 va 9-state’da turibmiz.
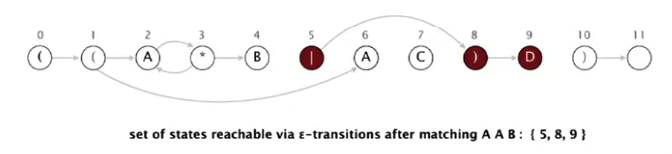
8. To’rtinchi (ohirgi) belgi – D faqat 9-state’da mavjud. 9-state’dan 10-state’ga match transition bor. Shunday qilib, AABD dan keyin biz 10-state’ga keldik.
9. 10-state’dan 11-state’ga epsilon transition bor. Hozir biz 10 va 11-state’da turibmiz. 11-state accept state bo’lgani uchun simulyatsiyani to’xtatamiz.
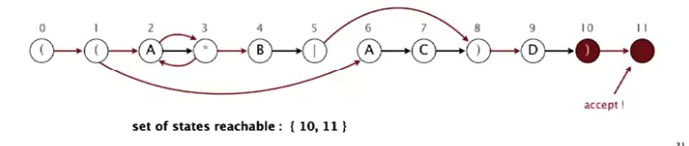
Xulosa – AABD matni ((A*B|AC)D) regexp uchun mos kelar ekan.
