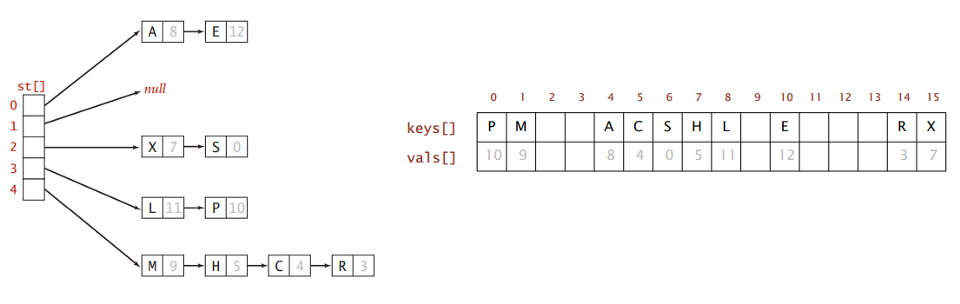
Collision deb hash funksiyaning turli xil key’lar uchun bir xil hash generatsiya qilishiga aytiladi. Amaliy tajribalar shuni ko’rsatadiki, hattoki eng yaxshi kriptografik algoritmlar yordamida generatsiya qilingan hash’da ham collision bo’lish ehtimoli kichik bo’lsada mavjud.
Agar biz o’zimiz hash funksiya yozadigan bo’lsak, albatta collision’da nima qilish kerakligini ham aniqlab olishimiz kerak. Collision’ning yechimi sifatida ikki usul keltirilgan: Separate chaining va Linear probing.
Separate chaining
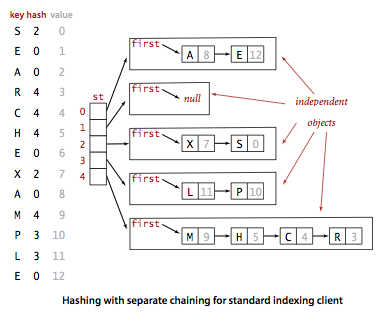
Separate chaining (alohida zanjirlar) – key’larni index’ga to’g’ridan to’g’ri bog’lamay, linked list yordamida bog’lab qo’yish nazarda tutiladi. Masalan, separate chaining usulida biz hash table‘da ko’rib o’tganimiz
hashmap[hash] = key
emas,
hashmap[hash] = Node {
key: key,
next: null }
ko’rinishida ifodalanadi. Hash table’ga key qo’shish vaqtida collision paydo bo’lsa, ya’ni generatsiya qilingan hash kod bo’sh bo’lmasa, qo’shilayotgan key, mavjud key’ga bog’lanadi.
hashmap[hash] = Node {
key: key1,
next: Node {
key: key2,
next: null
} }
Qidirishda ham hashmap[hash] dagi linked list ichidan key qidiriladi. Oson va samarali usul!
Linear probing
Collision muammosining yechimi uchun yana bir usul – Linear probing (chiziqli tekshirish).

Bunda agar hashmap[hash] bo’sh bo’lmasa, key hashmap[hash] dan keyingi slotga qo’yiladi – hashmap[hash + 1]. hashmap[hash + 1] ham bo’sh bo’lmasa, u holda hashmap[hash + 2] ga. Shu tariqa collision bo’lganda, key hashmap[hash] dan keyingi bo’sh indeksda saqlanadi. Qidirishda ham hashmap[hash] da berilgan key qidirilayotgan key’ga to’g’ri kelmasa hashmap[hash + 1] va hk tekshiriladi. Agar hashmap[hash + 1] bo’sh bo’lsa, demak key hash table’da mavjud emas – qidiruv tugaydi.
Linear probing ‘ni kamchiligi – key’ni hash table’dan o’chirgandan keyin paydo bo’ladigan muammosida. Agar key hashmap[hash + 2] da turgan bo’lsayu, hashmap[hash] o’chirilsa, keyin hashmap[hash + 1] va hashmap[hash + 2] ni topish mumkin bo’lmay qoladi. Shu sababli key o’chirilgach, undan keyingi elementlarni joyini surib chiqish kerak bo’ladi.
Separate chaining vs Linear probing
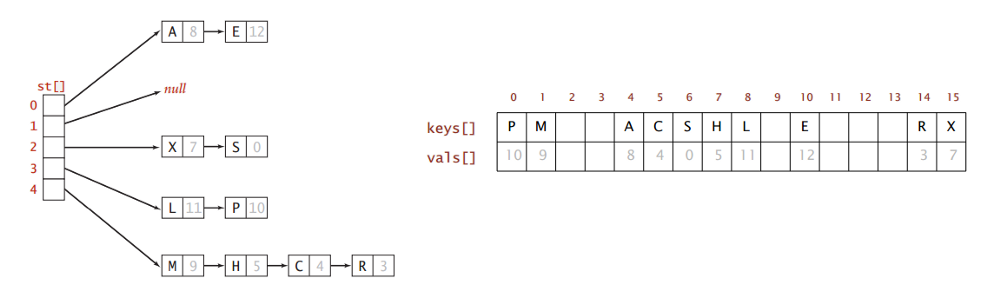
Kod yozish. Separate chaining da qo’shish (insert) va o’chirish (delete) ni amalga oshirish osonroq
Klastering. Separate chaining da yomon hash funksiya bilan ham kamroq muammo chiqadi.
Joy. Linear probing xotirada kamroq joy oladi, sababi Linear probing da Linked list yo’q, keyingi node’ga pointer yo’q – bular xotirani tejaydi.
Keshlash. Linear probing da keshlash samaraliroq. Sababi Linked list’ni o’qib chiqish protsessor keshini samarasiz.
O’qish (N/M). Barchasi kiritilayotgan key’larga va hash funksiyaga bog’liq.
Separate chaining da, agar key’lar uzunligi N ni hash indekslar soni M ga bo’lganimizda son kattalashib ketadigan bo’lsa (ya’ni bir xil hash kodli key’lar ko’p bo’lsa), u holda linked list’lar uzunlashib ketadi va key’ni o’qib olish ko’proq vaqt oladi. Odatda o’qish tezligi uchun N/M ~ 5 samarali deb baholanadi.
Linear probing da klasterlar – bir xil hash kodli key’lar ketma-ketligi uzun bo’lib ketsa, o’qish sekinlashadi.
Hash table vs Binary search tree
Hash table
- Kod yozishga osonroq
- Key’larning tartiblangan bo’lishi shartmas
- Oddiy key’lar uchun o’qish va yozish tez ishlaydi – O(N)
- Dasturlash tillarida tayyor yechimlar mavjud. Masalan hash table uchun Javascript’da Object yoki Map() dan foydalanish mumkin.
Binary search tree
- Kafolatlangan ishlash tezligi – O(log N)
- Tartiblash amallari (min, max, k-th min key) uchun qulay