Minimum spanning tree’ni topish uchun Kruskal algoritmi

Graph‘dagi minimum spanning tree‘ni topishning klassik algoritmlaridan biri – Kruskal algoritmi g’oyasi tushunishga oson. Uning ishlash tartibi:

1. Edge weight’larini o’sish tartibida saralab oladi.
2. Kichik edge’lardan boshlab, ularni graph’ga qo’shib boradi (qoraga bo’yab boradi). Agar edge qo’shilgach MSTda cycle hosil bo’lsa, edge’ni tushirib qoldiradi.
3. Ishni MSTdagi edge’lar soni V – 1 bo’lguncha davom ettiradi. V – graph’dagi vertex’lar soni.

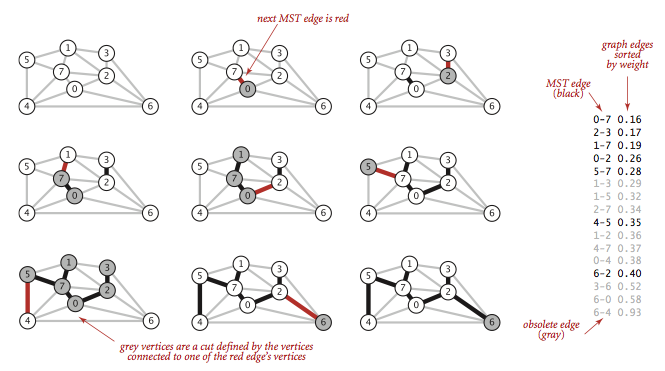
Kodda ifodalash

Kruskal algoritmini kodda ifodalashdan oldin quyidagi savollarga javob topish kerak.

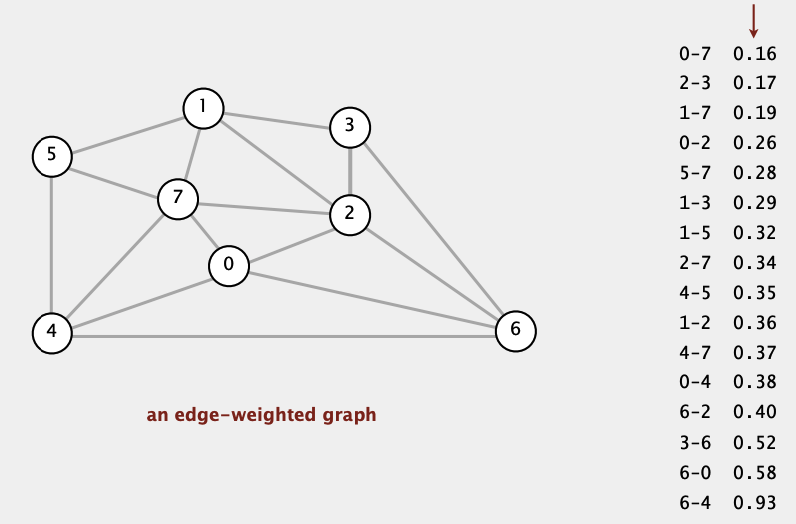
Edge weighted graph’ni qanday ifodalaymiz?

Edge weighted graph’ni adjacency list’da ifodalasa bo’ladi, faqat weight’ni ham qo’shib borish kerak. Menimcha bog’lanishlar uchun Map() mos keladi. Graph APIda biz Set() ni ishlatgan edik, sababi adjacency list uchun bog’langan vertex’ning indeksi kifoya qilardi. Endi bizga vertex va weight ham kerak bo’lgani uchun, edge’ning ikki uchi bo’lgan vertex’larni va weight’ni Map() da saqlaymiz.

const edges = new Map() // har bir edge uchun Map yaratamiz
edges.set('v', v) // v vertex
edges.set('w', w) // w vertex
edges.set('weight', weight) // w - v vertex'ga bog'langan boshqa vertex
graph[v] = edges

Agar biz 1 vertex’ga 4 vertex’ni 10 weight’li edge qilib bog’lasak, u holda adjacency list quyidagicha ko’rinishda bo’ladi:

graph[ null, Map { 'v': 0, 'w': 7, 'weight': 0.16 } ] // graph[0] = empty

Edge weight’larni o’sish tartibida qanday tartiblaymiz?

Javascript’da Array.sort() funksiyaning implementatsiyasida Mozilla MergeSort‘ni ishlatadi, Chrome V8 da esa QuickSort‘ni (kichik array’lar uchun Insertion sortni. Ikki algoritmning ham time complexity‘si bir xil bo’lgani uchun, biz tartiblashni optimallashtirish haqida o’ylab o’tirmay, Array.sort() dan foydalanamiz.

Cycle‘ni qanday aniqlaymiz?

Aylanalarni topish uchun depth first searchdan foydalansa bo’ladi. Aslida bizga cycle’ni topish ham shartmas, Edge’ning ikki vertexi – v dan w ga path borligini tekshirish kifoya qiladi. Sababi agar path bo’lsa, yangi qo’shiladigan edge cycle’ga olib keladi.

Path borligini tekshirish uchun depth first search‘dan foydalanish mumkin.

Alternativ variant – Union-Findni ishlatsa ham bo’ladi.

Kod

Quyidagi funksiya bog’lanishlarni Union-find‘da tekshiradi.

Kod Githubda: https://github.com/Webmaxor/leetcode-solutions/blob/master/algorithms/graphs/minimum-spanning-tree/kruskal-mst-with-union-find.js

* * *

Mavzu bo’yicha savollarni Github’dagi Webmaxor / leetcode-solutions repository’da yozishingiz yoki kodda Reference in new issue ni bosib, qoldirishingiz mumkin.