Endi biz DAGlar (directed acyclic graph) uchun shortest path‘ni topishni ko’rib chiqamiz. Aslida DAGlar uchun Dijkstra’ning algoritmi ham ishlayveradi, ammo bizdagi graph‘ning acyclic, ya’ni aylanasi yo’q ekanligini bilar ekanmiz, bu bizga shortest path’ni topish ishini yengillashtiradimi?
Qisqa javob – ha, shortest path’ni topish uchun, avval vertex’larni topological sort tartibida olib, ularga navbatma-navbat edge relaxation qo’llab chiqiladi. Graph DAG bo’lgani uchun, bizda aylanalar, ko’rilgan vertex’ga qaytib kelish ehtimoli bo’lmaydi. Topological sort va edge relaxation kombinatsiyasi bo’lgan algoritmning nomini acyclic shortest path deb ham ataladi.
Acyclic shortest path’ning Dijkstra algoritmidan qanday ustunlik taraflari bor?
- Boshlang’ich vertexdan boshqa vertex’larga qisqa yo’lni linear vaqt ichida topadi.
- Negativ weight’li edge’lar uchun ham ishlaydi. Dijkstra algoritmi negativ weight’lar uchun ishlamaydi.
- Longest path’ni topish (shortest path’ning teskarisi) masalalarida ham qo’l keladi.
Shortest path’ni topish uchun Dijkstra algoritmida ko’rib chiqqan graph’imiz DAG bo’lgani uchun bu yerda ham undan misol sifatida foydalanamiz.
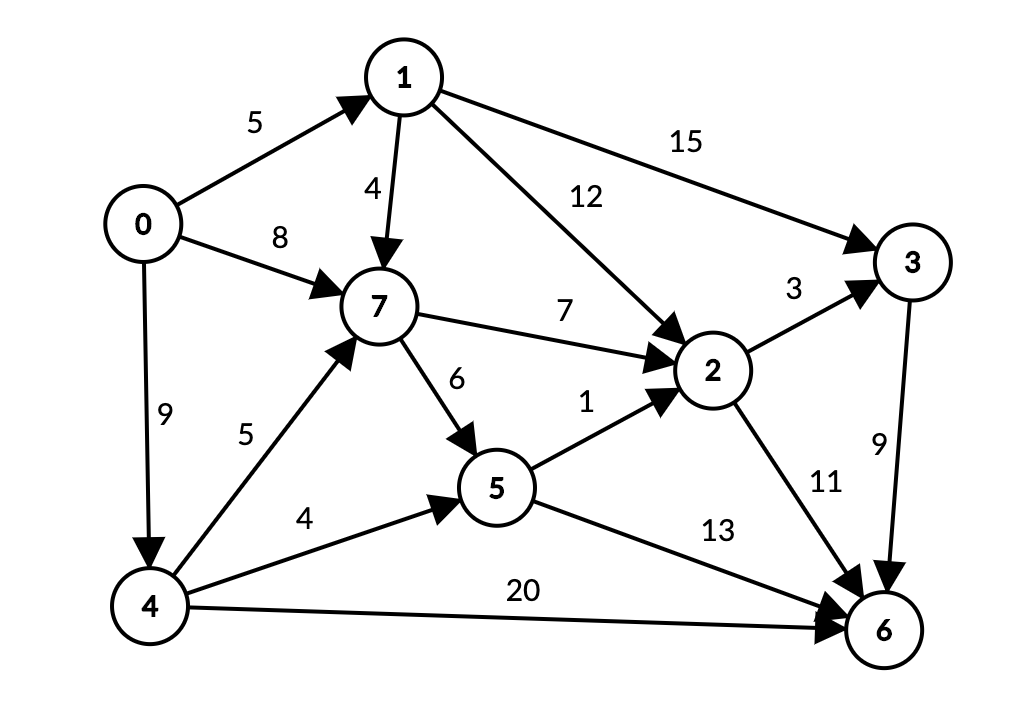
Graph uchun vertex’larning topological tartibi (topological sort’ni topish haqida):
[ 0, 1, 4, 7, 5, 2, 3, 6 ]
Biz har bir vertex uchun edge relaxation amalini qo’llab chiqamiz. Masofa va bog’lanishlarni odatdagidek distTo[] hamda edgeTo[] ga yig’ib boramiz.
Topological sort’dagi tartibga ko’ra, tekshirishni 0 vertex’dan boshlaymiz. 0 dan 1, 7 va 4 vertex’larga edge bor. Ular uchun 0 vertex’dan masofani hisoblaymiz.
| v | distTo | edgeTo |
|---|---|---|
| 0 | 0 | – |
| 1 | 5 | 0 |
| 2 | – | |
| 3 | – | |
| 4 | 9 | 0 |
| 5 | – | |
| 6 | – | |
| 7 | 8 | 0 |
Topological sort’dagi keyingi vertex – 1. 1 vertexdan davom ettiramiz.
1 dan 3, 2, 7 vertex’ga edge bor. Ular uchun boshlang’ich nuqta – 0 vertex’dan masofani hisoblaymiz.
| v | distTo[] | edgeTo[] |
|---|---|---|
| 0 | 0 | – |
| 1 | 5 | 0 |
| 2 | 5 + 12 = 17 | 1 |
| 3 | 5 + 17 = 20 | 1 |
| 4 | 9 | 0 |
| 5 | – | |
| 6 | – | |
| 7 | 8 | 0 |
0 -> 1 -> 7 masofasi = 9 chiqdi. Bizdagi 0 -> 7 masofa kichikroq – 8 ga teng. Shuning uchun 7 ga masofani yangilamaymiz. Faqat yangi masofa eskisidan kichik bo’lgandagina yangilanadi.
Keyingi vertex – 4. 4 dan 5, 6, 7 ga edge bor. Ular uchun boshlang’ich nuqta – 0 vertex’dan masofani hisoblaymiz.
| v | distTo[] | edgeTo[] |
|---|---|---|
| 0 | 0 | – |
| 1 | 5 | 0 |
| 2 | 17 | 1 |
| 3 | 20 | 1 |
| 4 | 9 | 0 |
| 5 | 9 + 4 = 13 | 4 |
| 6 | 9 + 20 = 29 | 4 |
| 7 | 8 | 0 |
Keyingi vertex – 7. 7 dan 2 va 5 vertex’ga edge bor. Ular uchun boshlang’ich nuqta – 0 vertex’dan masofani hisoblaymiz. 2-vertex uchun edge relaxation ishladi.
| v | distTo[] | edgeTo[] |
|---|---|---|
| 0 | 0 | – |
| 1 | 5 | 0 |
| 2 | 7 | |
| 3 | 20 | 1 |
| 4 | 9 | 0 |
| 5 | 13 | 4 |
| 6 | 29 | 4 |
| 7 | 8 | 0 |
Keyingi vertex – 5. 5 dan 2 va 6 vertex’ga edge bor. Ular uchun boshlang’ich nuqta – 0 vertex’dan masofani hisoblaymiz. 2 va 6 vertex’lar uchun edge relaxation ishladi.
| v | distTo[] | edgeTo[] |
|---|---|---|
| 0 | 0 | – |
| 1 | 5 | 0 |
| 2 | 5 | |
| 3 | 20 | 1 |
| 4 | 9 | 0 |
| 5 | 13 | 4 |
| 6 | 5 | |
| 7 | 8 | 0 |
Keyingi vertex – 2. 2 dan 3 va 6 vertex’ga edge bor. Ular uchun boshlang’ich nuqta – 0 vertex’dan masofani hisoblaymiz. 3 va 6 vertex’lar uchun edge relaxation ishladi.
| v | distTo[] | edgeTo[] |
|---|---|---|
| 0 | 0 | – |
| 1 | 5 | 0 |
| 2 | 14 | 5 |
| 3 | 2 | |
| 4 | 9 | 0 |
| 5 | 13 | 4 |
| 6 | 2 | |
| 7 | 8 | 0 |
Keyingi vertex – 3. 3 dan 6 vertex’ga edge bor. 0 dan 3 orqali 6 borish, 2 orqali borishdan kattaroq masofaga ega, shu sababli 6 yangilanmaydi.
Ohirgi vertex – 6 ning edge’lari yo’q, demak hisoblashlar tugadi. Yakuniy jadval quyidagicha bo’ladi.
| v | distTo | edgeTo |
|---|---|---|
| 0 | 0 | – |
| 1 | 5 | 0 |
| 2 | 14 | 5 |
| 3 | 17 | 2 |
| 4 | 9 | 0 |
| 5 | 13 | 4 |
| 6 | 25 | 2 |
| 7 | 8 | 0 |
Biz Dijkstra algoritmida bo’lgani kabi, bir xil natijaga erishdik:
Longest path qanday topiladi?
- Barcha weight’larni negativ qilib olinadi (weight * -1)
- Shortest path’lar topiladi
- Natijadagi weight’larni yana negativ qilib olinadi.
Shunda, minus qiymatdagi shortest path’lar plyusga aylantirilganda longest path’lar paydo bo’ladi.
Kod
Longest path’ni topish uchun graph’ga edge berish vaqtida negativ qiymatga o’zgartirish kifoya:
// Add weight
edge.set('weight', item[1] * -1)
Keyin distTo qiymatlarini agar keyinchalik ishlatilsa, u ham negativ qiymatga o’zgartiriladi. Aniqrog’i distTo dagi minusli weight’lar -1 ga ko’paytirilib, plyus qiymatga aylantiriladi.
Kod Githubda:
DAG shortest path: https://github.com/Webmaxor/leetcode-solutions/blob/master/algorithms/graphs/shortest-path/dag-shortest-path.js
DAG longest path: https://github.com/Webmaxor/leetcode-solutions/blob/master/algorithms/graphs/shortest-path/dag-longest-path.js
* * *
Mavzu bo’yicha savollarni Github’dagi Webmaxor / leetcode-solutions repository’da yozishingiz yoki kodda Reference in new issue ni bosib, qoldirishingiz mumkin.